


Next: 5 Observational tests of
Up: Abstract
Previous: 3 Constraints upon the
In order to examine the characteristics of the m=1 eigenmodes
confined to the inner part of the disc,
we have numerically solved Eqs. (16) and (17)
with boundary conditions
for a wide range of parameter values:
We surveyed eigenmodes
for a deformation factor of 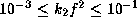 ,
radiative parameters of
,
radiative parameters of 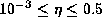 and
and
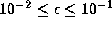 ,
disc temperature of
,
disc temperature of 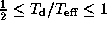 ,
density gradient index of
,
density gradient index of 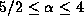 ,
and central stars with spectral types of B0V and B5V.
Since we found that the obtained eigenmodes are roughly similar
for different values of disc parameters and
,
and central stars with spectral types of B0V and B5V.
Since we found that the obtained eigenmodes are roughly similar
for different values of disc parameters and  ,
we restrict our attention to cases with
,
we restrict our attention to cases with
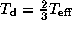 ,
, 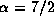 ,
and
,
and 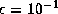 .
.
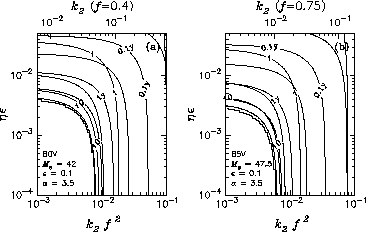
Fig.2: Distribution of the period and
the propagation-region width of
the fundamental mode confined to
the inner part of the disc around
a a B0V star and b a B5V star.
Thick contours denote the oscillation period
in units of years and thin contours denote
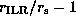 .
The interval of contours is 0.5dex.
Scales for
.
The interval of contours is 0.5dex.
Scales for 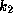 are also shown for
a
are also shown for
a 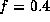 and b
and b 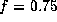 .
The ragged boundary denotes the critical curve below which
no confined eigenmode is found
.
The ragged boundary denotes the critical curve below which
no confined eigenmode is found
Figure 2 shows the distribution of
the two characteristic quantities,
the period of the oscillation and the size of the propagation region,
of the fundamental
m=1 eigenmodes confined to the inner part of the disc.
Figure 2(a) is for a B0V star and
Fig. 2(b) for a B5V star.
Other values of parameters are annotated in the figure.
In each figure thick contours denote the oscillation period
in units of years and thin contours denote 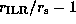 ,
where
,
where 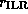 is the radius of the inner Lindblad resonance.
Recall that
is the radius of the inner Lindblad resonance.
Recall that 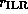 is a good measure of the width of
the propagation region of the eigenmode.
The interval of contours is 0.5dex.
At the top of each panel
we show the scale for
is a good measure of the width of
the propagation region of the eigenmode.
The interval of contours is 0.5dex.
At the top of each panel
we show the scale for 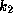 for (a)
for (a) 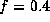 and (b)
and (b) 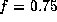 .
The ragged boundary in each figure denotes the critical curve
discussed in the previous section;
we found no confined eigenmode for the values of
.
The ragged boundary in each figure denotes the critical curve
discussed in the previous section;
we found no confined eigenmode for the values of
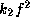 and
and 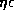 below this line.
As mentioned earlier, the raggedness of the critical curve
reflects that we surveyed the (
below this line.
As mentioned earlier, the raggedness of the critical curve
reflects that we surveyed the (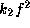 ,
, 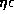 )-space
with a resolution of 0.02dex.
)-space
with a resolution of 0.02dex.
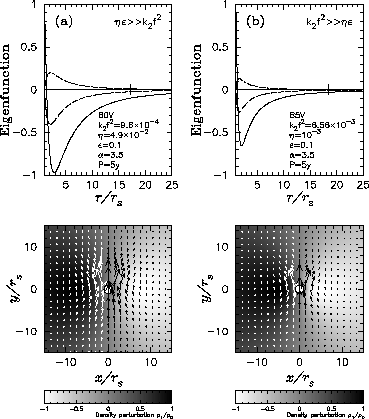
Fig.3: Fundamental mode for a 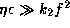 and b
and b 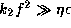 .
The disc
temperature is
.
The disc
temperature is 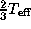 .
The values of the other parameters are indicated
in the upper panel.
In the upper panel,
the solid, dashed, and dash-dotted lines denote
.
The values of the other parameters are indicated
in the upper panel.
In the upper panel,
the solid, dashed, and dash-dotted lines denote
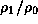 ,
, 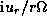 , and
, and
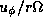 , respectively.
The location of the inner Lindblad resonance is
shown by the vertical bar.
In the lower panel, the gray-scale plot denotes
the density perturbation
, respectively.
The location of the inner Lindblad resonance is
shown by the vertical bar.
In the lower panel, the gray-scale plot denotes
the density perturbation 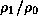 in the
in the 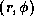 -plane,
while arrows denote the perturbed-velocity vectors
(
-plane,
while arrows denote the perturbed-velocity vectors
(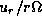 ,
, 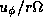 )
)
From Fig. 2, we note that the period of the eigenmode
is sensitive to
the parameters characterizing the rotational deformation
and the weak line force.
It rapidly decreases with increasing values of
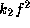 or
or 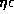 .
The dependence of the period on these parameters
is similar for different values of
.
The dependence of the period on these parameters
is similar for different values of  and
and 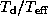 (or equivalently
(or equivalently 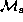 ),
except that, as the pressure effect decreases,
the critical curve in the (
),
except that, as the pressure effect decreases,
the critical curve in the (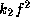 ,
, 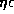 )-plane
moves to the lower left and
modes with longer periods appear.
Needless to say,
the period of the confined mode is independent of the disc outer radius
as long as it is located far outside the propagation region of the mode.
Consequently, the range of observed periods of the V/R variations
places a rather narrow constraint on
)-plane
moves to the lower left and
modes with longer periods appear.
Needless to say,
the period of the confined mode is independent of the disc outer radius
as long as it is located far outside the propagation region of the mode.
Consequently, the range of observed periods of the V/R variations
places a rather narrow constraint on 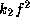 and
and 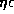 .
Suppose that the observed periods range from a year to a decade
both for B0- and for B5-type Be stars.
Suppose also that the radiative effect is dominant in discs
of B0-type Be stars, while the rotational effect is dominant in discs
of B5-type Be stars.
Then, the range of
.
Suppose that the observed periods range from a year to a decade
both for B0- and for B5-type Be stars.
Suppose also that the radiative effect is dominant in discs
of B0-type Be stars, while the rotational effect is dominant in discs
of B5-type Be stars.
Then, the range of 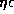 for B0-type Be stars and
the range of
for B0-type Be stars and
the range of 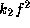 for B5-type Be stars are, respectively,
restricted to
for B5-type Be stars are, respectively,
restricted to
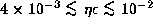 and
and
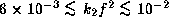 .
If a star exhibits a V/R variation with a period longer than
a decade,
it indicates that the pressure effect in the disc would also be weaker
than that adopted in Fig. 2,
i.e.,
.
If a star exhibits a V/R variation with a period longer than
a decade,
it indicates that the pressure effect in the disc would also be weaker
than that adopted in Fig. 2,
i.e., 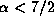 and/or
and/or 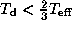 .
.
Now we discuss the characteristics of the eigenmodes
confined to the inner part of Be-star discs.
Figure 3 presents two examples of the fundamental
m=1 modes.
Figure 3(a) is for the radiation-effect dominant case
for a B0V star, while
Fig. 3(b) is for the rotation-effect dominant case
for a B5V star.
In this example, both modes have the same period of 5 years.
The adopted disc temperature is 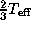 .
The values of the other parameters are indicated in the upper panels.
In each upper panel,
the solid, dashed, and dash-dotted lines denote
.
The values of the other parameters are indicated in the upper panels.
In each upper panel,
the solid, dashed, and dash-dotted lines denote
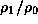 ,
, 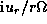 , and
, and
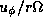 , respectively.
They are normalized such that
the maximum value of
, respectively.
They are normalized such that
the maximum value of 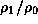 is unity.
The vertical bar denotes the location of
the inner Lindblad resonance.
Note that
is unity.
The vertical bar denotes the location of
the inner Lindblad resonance.
Note that 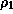 and
and 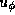 vary as
vary as
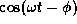 ,
while
,
while 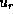 varies as
varies as 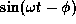 .
The lower panels show the distribution of
these quantities in the inner
.
The lower panels show the distribution of
these quantities in the inner 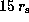 in the
in the 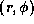 -plane.
The circle at the center denotes the location of
the star/disc interface.
The perturbation pattern as well as the unperturbed disc
rotates counterclockwise.
The density perturbation
-plane.
The circle at the center denotes the location of
the star/disc interface.
The perturbation pattern as well as the unperturbed disc
rotates counterclockwise.
The density perturbation 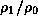 is denoted by
a gray-scale representation.
Arrows superposed on the gray-scale plot are
the perturbed-velocity vectors (
is denoted by
a gray-scale representation.
Arrows superposed on the gray-scale plot are
the perturbed-velocity vectors (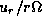 ,
, 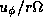 ).
The length of each arrow is proportional to
the strength of the perturbation.
).
The length of each arrow is proportional to
the strength of the perturbation.
From the upper panels of Fig. 3,
we note that in both cases
the fundamental m=1 modes are well confined
to the inner part of the disc.
We also note that the global features of the eigenfunctions are
very similar in both cases, except that
the region in which the amplitude of the perturbation
is large is slightly narrower in the rotation-effect dominant case
than in the radiation-effect dominant case.
The azimuthal component of the velocity perturbation 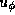 anticorrelates with
the density perturbation
anticorrelates with
the density perturbation 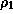 ,
except in the innermost narrow part of the disc.
Note that this property, which was also seen in the modes
studied in Okazaki (1991),
has been shown to cause the observed line-profile variability
of the V/R variations
(Hummel & Hanuschik 1994, 1996; Hanuschik et al. 1995; Okazaki 1996).
,
except in the innermost narrow part of the disc.
Note that this property, which was also seen in the modes
studied in Okazaki (1991),
has been shown to cause the observed line-profile variability
of the V/R variations
(Hummel & Hanuschik 1994, 1996; Hanuschik et al. 1995; Okazaki 1996).



Next: 5 Observational tests of
Up: Abstract
Previous: 3 Constraints upon the
Atsuo Okazaki
平成9年3月15日 (土), 午後 1時19分3秒
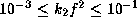 ,
radiative parameters of
,
radiative parameters of 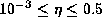 and
and
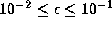 ,
disc temperature of
,
disc temperature of 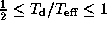 ,
density gradient index of
,
density gradient index of 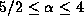 ,
and central stars with spectral types of B0V and B5V.
Since we found that the obtained eigenmodes are roughly similar
for different values of disc parameters and
,
and central stars with spectral types of B0V and B5V.
Since we found that the obtained eigenmodes are roughly similar
for different values of disc parameters and  ,
we restrict our attention to cases with
,
we restrict our attention to cases with
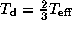 ,
, 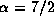 ,
and
,
and 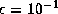 .
.

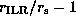 .
The interval of contours is 0.5dex.
Scales for
.
The interval of contours is 0.5dex.
Scales for 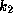 are also shown for
a
are also shown for
a 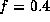 and b
and b 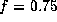 .
The ragged boundary denotes the critical curve below which
no confined eigenmode is found
.
The ragged boundary denotes the critical curve below which
no confined eigenmode is found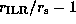 ,
where
,
where 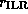 is the radius of the inner Lindblad resonance.
Recall that
is the radius of the inner Lindblad resonance.
Recall that 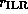 is a good measure of the width of
the propagation region of the eigenmode.
The interval of contours is 0.5dex.
At the top of each panel
we show the scale for
is a good measure of the width of
the propagation region of the eigenmode.
The interval of contours is 0.5dex.
At the top of each panel
we show the scale for 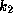 for (a)
for (a) 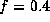 and (b)
and (b) 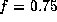 .
The ragged boundary in each figure denotes the critical curve
discussed in the previous section;
we found no confined eigenmode for the values of
.
The ragged boundary in each figure denotes the critical curve
discussed in the previous section;
we found no confined eigenmode for the values of
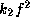 and
and 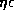 below this line.
As mentioned earlier, the raggedness of the critical curve
reflects that we surveyed the (
below this line.
As mentioned earlier, the raggedness of the critical curve
reflects that we surveyed the (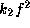 ,
, 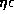 )-space
with a resolution of 0.02dex.
)-space
with a resolution of 0.02dex.

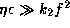 and b
and b 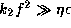 .
The disc
temperature is
.
The disc
temperature is 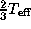 .
The values of the other parameters are indicated
in the upper panel.
In the upper panel,
the solid, dashed, and dash-dotted lines denote
.
The values of the other parameters are indicated
in the upper panel.
In the upper panel,
the solid, dashed, and dash-dotted lines denote
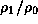 ,
, 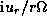 , and
, and
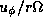 , respectively.
The location of the inner Lindblad resonance is
shown by the vertical bar.
In the lower panel, the gray-scale plot denotes
the density perturbation
, respectively.
The location of the inner Lindblad resonance is
shown by the vertical bar.
In the lower panel, the gray-scale plot denotes
the density perturbation 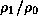 in the
in the 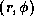 -plane,
while arrows denote the perturbed-velocity vectors
(
-plane,
while arrows denote the perturbed-velocity vectors
(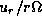 ,
, 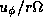 )
)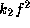 or
or 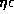 .
The dependence of the period on these parameters
is similar for different values of
.
The dependence of the period on these parameters
is similar for different values of  and
and 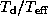 (or equivalently
(or equivalently 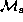 ),
except that, as the pressure effect decreases,
the critical curve in the (
),
except that, as the pressure effect decreases,
the critical curve in the (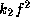 ,
, 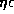 )-plane
moves to the lower left and
modes with longer periods appear.
Needless to say,
the period of the confined mode is independent of the disc outer radius
as long as it is located far outside the propagation region of the mode.
Consequently, the range of observed periods of the V/R variations
places a rather narrow constraint on
)-plane
moves to the lower left and
modes with longer periods appear.
Needless to say,
the period of the confined mode is independent of the disc outer radius
as long as it is located far outside the propagation region of the mode.
Consequently, the range of observed periods of the V/R variations
places a rather narrow constraint on 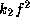 and
and 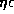 .
Suppose that the observed periods range from a year to a decade
both for B0- and for B5-type Be stars.
Suppose also that the radiative effect is dominant in discs
of B0-type Be stars, while the rotational effect is dominant in discs
of B5-type Be stars.
Then, the range of
.
Suppose that the observed periods range from a year to a decade
both for B0- and for B5-type Be stars.
Suppose also that the radiative effect is dominant in discs
of B0-type Be stars, while the rotational effect is dominant in discs
of B5-type Be stars.
Then, the range of 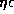 for B0-type Be stars and
the range of
for B0-type Be stars and
the range of 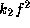 for B5-type Be stars are, respectively,
restricted to
for B5-type Be stars are, respectively,
restricted to
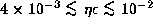 and
and
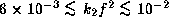 .
If a star exhibits a V/R variation with a period longer than
a decade,
it indicates that the pressure effect in the disc would also be weaker
than that adopted in Fig.
.
If a star exhibits a V/R variation with a period longer than
a decade,
it indicates that the pressure effect in the disc would also be weaker
than that adopted in Fig. 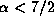 and/or
and/or 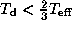 .
.
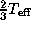 .
The values of the other parameters are indicated in the upper panels.
In each upper panel,
the solid, dashed, and dash-dotted lines denote
.
The values of the other parameters are indicated in the upper panels.
In each upper panel,
the solid, dashed, and dash-dotted lines denote
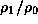 ,
, 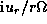 , and
, and
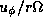 , respectively.
They are normalized such that
the maximum value of
, respectively.
They are normalized such that
the maximum value of 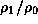 is unity.
The vertical bar denotes the location of
the inner Lindblad resonance.
Note that
is unity.
The vertical bar denotes the location of
the inner Lindblad resonance.
Note that 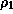 and
and 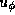 vary as
vary as
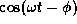 ,
while
,
while 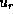 varies as
varies as 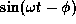 .
The lower panels show the distribution of
these quantities in the inner
.
The lower panels show the distribution of
these quantities in the inner 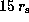 in the
in the 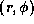 -plane.
The circle at the center denotes the location of
the star/disc interface.
The perturbation pattern as well as the unperturbed disc
rotates counterclockwise.
The density perturbation
-plane.
The circle at the center denotes the location of
the star/disc interface.
The perturbation pattern as well as the unperturbed disc
rotates counterclockwise.
The density perturbation 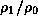 is denoted by
a gray-scale representation.
Arrows superposed on the gray-scale plot are
the perturbed-velocity vectors (
is denoted by
a gray-scale representation.
Arrows superposed on the gray-scale plot are
the perturbed-velocity vectors (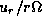 ,
, 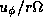 ).
The length of each arrow is proportional to
the strength of the perturbation.
).
The length of each arrow is proportional to
the strength of the perturbation.
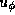 anticorrelates with
the density perturbation
anticorrelates with
the density perturbation 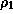 ,
except in the innermost narrow part of the disc.
Note that this property, which was also seen in the modes
studied in Okazaki (1991),
has been shown to cause the observed line-profile variability
of the V/R variations
(Hummel & Hanuschik 1994, 1996; Hanuschik et al. 1995; Okazaki 1996).
,
except in the innermost narrow part of the disc.
Note that this property, which was also seen in the modes
studied in Okazaki (1991),
has been shown to cause the observed line-profile variability
of the V/R variations
(Hummel & Hanuschik 1994, 1996; Hanuschik et al. 1995; Okazaki 1996).