
It is instructive to examine the set of Eqs. (16) and (17) semi-analytically by an asymptotic method, before solving them numerically. For this purpose, we transform Eqs. (16) and (17) into the form
where
under the approximations 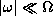 ,
,
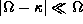 , and
, and 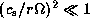 .
In Eq. (20),
.
In Eq. (20),
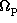 is the local precession frequency given by
is the local precession frequency given by
Equation (20) expresses the dispersion relation
by which we can converniently discuss
some of the characteristics of the eigenmodes.
Local oscillations can propagate in regions where 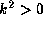 ,
while they are evanescent in regions where
,
while they are evanescent in regions where 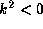 .
The value of
.
The value of 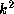 increases monotonically with decreasing
increases monotonically with decreasing  over the frequency range
over the frequency range 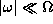 in the current problem.
When
in the current problem.
When 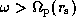 ,
the value of
,
the value of 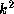 is negative throughout the disc.
No eigenmodes are thus present within this frequency range.
On the other hand, when
is negative throughout the disc.
No eigenmodes are thus present within this frequency range.
On the other hand, when 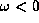 ,
the propagation region extends over the entire disc
if a moderate value of
,
the propagation region extends over the entire disc
if a moderate value of  is adopted.
As pointed out by PSH and SH,
the retrograde modes (i.e., modes with
is adopted.
As pointed out by PSH and SH,
the retrograde modes (i.e., modes with 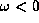 )
are thus not confined to the inner part of the disc.
Therefore, the eigenfrequency
)
are thus not confined to the inner part of the disc.
Therefore, the eigenfrequency  for
the m=1 oscillation confined to the inner part of the disc
is found in the range
for
the m=1 oscillation confined to the inner part of the disc
is found in the range
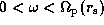 ,
for which the propagation region lies between
,
for which the propagation region lies between 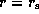 and the turning-point radius at which
and the turning-point radius at which 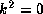 .
.
The asymptotic form of the eigenfunction Y, which satisfies the boundary conditions described in the previous section, is written as
where k, given by Eq. (20), must satisfy the following eigenvalue condition
with a non-negative integer n.
In the above equations, 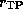 is the radius
of the turning point.
Note that
is the radius
of the turning point.
Note that 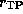 approximately coincides with
the radius of the inner Lindblad resonance
approximately coincides with
the radius of the inner Lindblad resonance 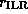 at which
at which 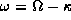 [for details of the modal analysis by an asymptotic method,
see Sect. 16 of Unno et al. (1989)].
[for details of the modal analysis by an asymptotic method,
see Sect. 16 of Unno et al. (1989)].
Fig.1: Critical lines in the (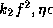 )-plane
below which no confinement of m=1 oscillations
occurs in discs around a a typical B0V star and
b a typical B5V star.
The values of the disc parameters are annotated.
The value of
)-plane
below which no confinement of m=1 oscillations
occurs in discs around a a typical B0V star and
b a typical B5V star.
The values of the disc parameters are annotated.
The value of  is fixed to be 0.1.
Scales for
is fixed to be 0.1.
Scales for 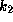 are also shown
for a
are also shown
for a 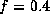 and b
and b 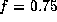
Equations (20)--(23) show that,
with increasing 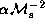 ,
,
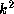 decreases and the mode becomes less confined.
This confirms the discussion by PSH and SH
that the pressure effect acts against the confinement.
This also means that,
for a given value of
decreases and the mode becomes less confined.
This confirms the discussion by PSH and SH
that the pressure effect acts against the confinement.
This also means that,
for a given value of 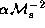 ,
there is a critical curve in the (
,
there is a critical curve in the (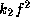 ,
, 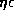 )-plane
below which no confinement of oscillations occurs.
Our interest is then how large a value of
)-plane
below which no confinement of oscillations occurs.
Our interest is then how large a value of 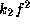 or
or 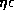 is needed to give rise to the confinement of the m=1 oscillations.
Figure 1 shows such critical curves
in the (
is needed to give rise to the confinement of the m=1 oscillations.
Figure 1 shows such critical curves
in the (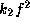 ,
, 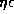 )-plane
below which we find no numerical solution for
Eqs. (16) and (17) given
the boundary conditions.
Figure 1(a) is for a B0V star and
Fig. 1(b) for a B5V star.
The values of the disc parameters are attached to each line.
The thick line in each figure denotes the critical curve
for
)-plane
below which we find no numerical solution for
Eqs. (16) and (17) given
the boundary conditions.
Figure 1(a) is for a B0V star and
Fig. 1(b) for a B5V star.
The values of the disc parameters are attached to each line.
The thick line in each figure denotes the critical curve
for 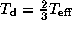 and
and 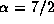 ,
which we regard as typical values for Be-star discs.
The raggedness of each line reflects that
we surveyed the (
,
which we regard as typical values for Be-star discs.
The raggedness of each line reflects that
we surveyed the (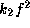 ,
, 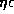 )-space with a resolution
of 0.02dex.
For the sake of convenience,
we also show the scales of
)-space with a resolution
of 0.02dex.
For the sake of convenience,
we also show the scales of 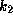 for
for 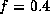 [Fig. 1(a)] and
for
[Fig. 1(a)] and
for 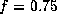 [Fig. 1(b)],
which are taken as typical values
for actual Be stars.
Though Fig. 1 is plotted for
[Fig. 1(b)],
which are taken as typical values
for actual Be stars.
Though Fig. 1 is plotted for 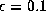 ,
the results are insensitive to the value of
,
the results are insensitive to the value of  ,
as long as
,
as long as 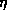 ,
, 
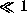 .
.
From Fig. 1
we observe that the critical curve in
the (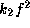 ,
, 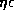 )-plane
above which the confinement occurs moves upward
with increasing importance of the pressure effect.
We also observe that, for parameters of a typical B0-type Be star
[Fig. 1(a)],
no m=1 oscillations are confined
without the contribution of the radiative force,
unless
)-plane
above which the confinement occurs moves upward
with increasing importance of the pressure effect.
We also observe that, for parameters of a typical B0-type Be star
[Fig. 1(a)],
no m=1 oscillations are confined
without the contribution of the radiative force,
unless 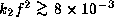 (i.e.,
(i.e., 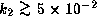 for
for 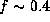 )
for
)
for 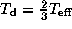 and
and 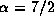 (thick line).
Even for the case of the weakest pressure effect
(
(thick line).
Even for the case of the weakest pressure effect
(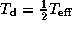 and
and 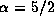 ),
the confinement of oscillations without the radiative effect
requires
),
the confinement of oscillations without the radiative effect
requires 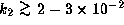 .
It is unlikely that B0-type Be stars have such large values of
.
It is unlikely that B0-type Be stars have such large values of 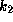 ,
because they appear not to be extreme rotators.
Adopting
,
because they appear not to be extreme rotators.
Adopting 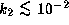 ,
, 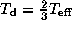 ,
and
,
and 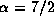 ,
we obtain that
the confinement of the m=1 oscillations requires a radiative effect
as large as
,
we obtain that
the confinement of the m=1 oscillations requires a radiative effect
as large as 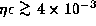 .
Note that this value of
.
Note that this value of 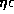 is not unreasonable,
if
is not unreasonable,
if 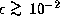 .
We conclude that it is the radiative effect that is important
for the confinement of the m=1 oscillations in discs
around B0-type Be stars.
The rotational effect is minor for these stars.
.
We conclude that it is the radiative effect that is important
for the confinement of the m=1 oscillations in discs
around B0-type Be stars.
The rotational effect is minor for these stars.
On the other hand,
for B5-type Be stars [Fig. 1(b)],
the rotational effect seems large enough to
confine the m=1 oscillations.
In a typical B5-type Be star disc
(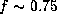 ,
, 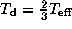 , and
, and 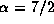 ),
the m=1 oscillations are confined
without any contribution of the radiative effect,
if
),
the m=1 oscillations are confined
without any contribution of the radiative effect,
if 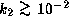 .
This value of
.
This value of 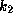 is reasonable, because
the rotational deformation of a B5-type Be star
is expected to be, on average,
much larger than that of a B0-type Be star.
Moreover,
since the luminosity of a B5-type star is about 10 times smaller than
that of a B0-type star,
the effect due to the radiative force would play a minor role
in a B5-type star.
In such discs,
the effect of rotational deformation of the star is therefore
much more important than the radiative effect.
is reasonable, because
the rotational deformation of a B5-type Be star
is expected to be, on average,
much larger than that of a B0-type Be star.
Moreover,
since the luminosity of a B5-type star is about 10 times smaller than
that of a B0-type star,
the effect due to the radiative force would play a minor role
in a B5-type star.
In such discs,
the effect of rotational deformation of the star is therefore
much more important than the radiative effect.