


Next: 3 Constraints upon the
Up: 2 The unperturbed disc
Previous: 2.1 Unperturbed disc model
A linear m=1 perturbation which varies as
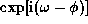 is superposed on
the unperturbed disc described above.
The perturbation is assumed to be isothermal,
because in a Be-star disc the thermal time-scale is
much shorter than the dynamical time-scale.
In the following equations describing the perturbation,
we treat only the lowest-order terms with respect to
the vertical coordinate z.
These assumptions and procedures are the same as those adopted
in Okazaki (1991).
Then, the linearized equations describing
the mass, momentum, and angular momentum conservation are
is superposed on
the unperturbed disc described above.
The perturbation is assumed to be isothermal,
because in a Be-star disc the thermal time-scale is
much shorter than the dynamical time-scale.
In the following equations describing the perturbation,
we treat only the lowest-order terms with respect to
the vertical coordinate z.
These assumptions and procedures are the same as those adopted
in Okazaki (1991).
Then, the linearized equations describing
the mass, momentum, and angular momentum conservation are
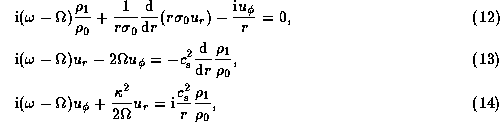
where 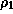 is the Eulerian perturbation of the density,
is the Eulerian perturbation of the density,
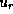 and
and 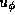 the horizontal velocity components
associated with the perturbation,
and
the horizontal velocity components
associated with the perturbation,
and 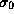 the surface density given by
the surface density given by
[for details of deriving
Eqs. (12)--(14),
see Okazaki (1991)].
Eliminating 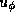 from Eqs. (12)--(14),
we obtain the following set of equations:
from Eqs. (12)--(14),
we obtain the following set of equations:
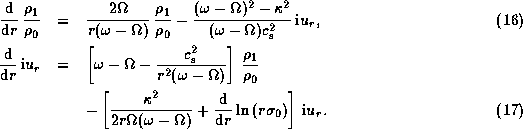
Equations (16) and (17) are
the basic equations for
the linear, one-armed isothermal oscillations in the disc.
Note that Eqs. (16) and (17)
are essentially the same as those used
in Okazaki (1991) and SH,
except that, through 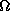 and
and  ,
our equations implicitly depend on the effect due to
the radiative force as well as
due to the rotational deformation of the star.
,
our equations implicitly depend on the effect due to
the radiative force as well as
due to the rotational deformation of the star.
We now consider the boundary conditions to be imposed on
Eqs. (16) and (17).
The eigenmode of interest is the mode confined to
the inner part of the disc.
Since the mode must be evanescent in the outer part,
we adopt
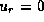 at some large radius
at some large radius 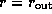 as the outer boundary condition.
We impose the inner boundary condition at the star/disc interface
as the outer boundary condition.
We impose the inner boundary condition at the star/disc interface
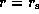 .
Since the pressure scale-height of the star near the interface
is much smaller than that of the disc,
the waves in the disc do not penetrate the stellar surface.
Hence, we take
.
Since the pressure scale-height of the star near the interface
is much smaller than that of the disc,
the waves in the disc do not penetrate the stellar surface.
Hence, we take
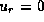 at
at 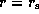 as the inner boundary condition.
as the inner boundary condition.



Next: 3 Constraints upon the
Up: 2 The unperturbed disc
Previous: 2.1 Unperturbed disc model
Atsuo Okazaki
平成9年3月15日 (土), 午後 1時19分3秒
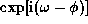 is superposed on
the unperturbed disc described above.
The perturbation is assumed to be isothermal,
because in a Be-star disc the thermal time-scale is
much shorter than the dynamical time-scale.
In the following equations describing the perturbation,
we treat only the lowest-order terms with respect to
the vertical coordinate z.
These assumptions and procedures are the same as those adopted
in Okazaki (1991).
Then, the linearized equations describing
the mass, momentum, and angular momentum conservation are
is superposed on
the unperturbed disc described above.
The perturbation is assumed to be isothermal,
because in a Be-star disc the thermal time-scale is
much shorter than the dynamical time-scale.
In the following equations describing the perturbation,
we treat only the lowest-order terms with respect to
the vertical coordinate z.
These assumptions and procedures are the same as those adopted
in Okazaki (1991).
Then, the linearized equations describing
the mass, momentum, and angular momentum conservation are
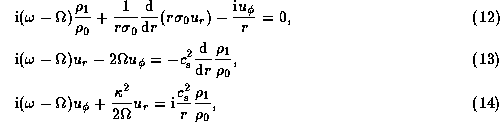
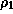 is the Eulerian perturbation of the density,
is the Eulerian perturbation of the density,
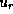 and
and 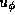 the horizontal velocity components
associated with the perturbation,
and
the horizontal velocity components
associated with the perturbation,
and 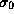 the surface density given by
the surface density given by
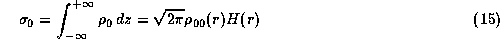
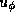 from Eqs. (
from Eqs. (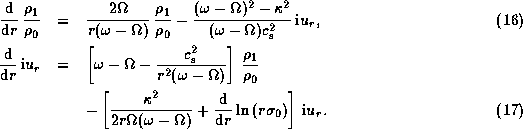
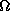 and
and  ,
our equations implicitly depend on the effect due to
the radiative force as well as
due to the rotational deformation of the star.
,
our equations implicitly depend on the effect due to
the radiative force as well as
due to the rotational deformation of the star.
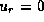 at some large radius
at some large radius 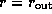 as the outer boundary condition.
We impose the inner boundary condition at the star/disc interface
as the outer boundary condition.
We impose the inner boundary condition at the star/disc interface
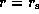 .
Since the pressure scale-height of the star near the interface
is much smaller than that of the disc,
the waves in the disc do not penetrate the stellar surface.
Hence, we take
.
Since the pressure scale-height of the star near the interface
is much smaller than that of the disc,
the waves in the disc do not penetrate the stellar surface.
Hence, we take
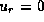 at
at 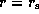 as the inner boundary condition.
as the inner boundary condition.