


Next: 2.2 Equations for one-armed
Up: 2 The unperturbed disc
Previous: 2 The unperturbed disc
We take a geometrically thin,
axisymmetric disc as an unperturbed equilibrium disc.
For simplicity, the disc is assumed to be isothermal
with a temperature range of
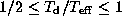 .
Here,
.
Here, 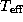 is the effective temperature of the star.
We also assume that the unperturbed disc is in hydrostatic equilibrium
in the vertical direction
and extends from the stellar surface (
is the effective temperature of the star.
We also assume that the unperturbed disc is in hydrostatic equilibrium
in the vertical direction
and extends from the stellar surface (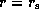 ) to infinity
in the radial direction.
We neglect radial advective motions and viscous effects.
The adopted value of the mean molecular weight is 0.6.
We use a cylindrical coordinate system
) to infinity
in the radial direction.
We neglect radial advective motions and viscous effects.
The adopted value of the mean molecular weight is 0.6.
We use a cylindrical coordinate system
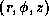 to describe the disc;
the origin is at the center of the star and
the z-axis is perpendicular to the disc midplane.
to describe the disc;
the origin is at the center of the star and
the z-axis is perpendicular to the disc midplane.
When the distortion of the star is weak,
the potential of the star of mass M with
apsidal motion constant 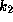 can be approximated as
can be approximated as
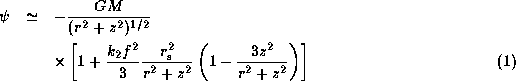
(PSH; SH).
Here, f is the rotation parameter, defined by
the ratio of the rotation velocity of the star
to the Keplerian velocity at the stellar surface.
According to Kogure & Hirata (1982),
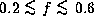 for B0-type Be stars
and
for B0-type Be stars
and 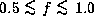 for B5-type Be stars.
The values of
for B5-type Be stars.
The values of 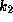 for rapidly rotating stars are not well known.
Theoretically,
for rapidly rotating stars are not well known.
Theoretically, 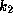 for non-rotating main-sequence stars has a
maximum value of
for non-rotating main-sequence stars has a
maximum value of 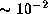 at a mass between 7 and
at a mass between 7 and 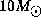 (Stothers 1974).
In general,
(Stothers 1974).
In general, 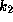 is a decreasing function of the degree of
the central condensation of the star:
The value of
is a decreasing function of the degree of
the central condensation of the star:
The value of 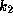 is smaller for a more evolved star
or for a star with larger uniform rotation
(Stothers 1974; Claret & Giménez 1993),
while it can be large for a star of which the inner part
rotates more rapidly than the outer part.
PSH adopted
is smaller for a more evolved star
or for a star with larger uniform rotation
(Stothers 1974; Claret & Giménez 1993),
while it can be large for a star of which the inner part
rotates more rapidly than the outer part.
PSH adopted 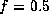 and
and
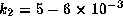 and SH studied the rotation effect
for
and SH studied the rotation effect
for 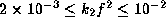 .
.
For the radiative force
we adopt the parametric form proposed by Chen & Marlborough (1994):
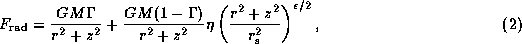
where 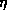 and
and  are parameters which characterize
the force due to an ensemble of optically thin lines.
According to Chen & Marlborough (1994),
are parameters which characterize
the force due to an ensemble of optically thin lines.
According to Chen & Marlborough (1994),
 should be a positive number which is much smaller than unity.
In the above expression,
should be a positive number which is much smaller than unity.
In the above expression,
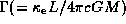 is the Eddington factor
that accounts for the reduction in the effective gravity
due to electron scattering.
Here,
is the Eddington factor
that accounts for the reduction in the effective gravity
due to electron scattering.
Here, 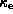 is the opacity due to electron scattering
per mass unit and L is the total luminosity of the star.
In the rest of this paper,
we neglect the Eddington factor
is the opacity due to electron scattering
per mass unit and L is the total luminosity of the star.
In the rest of this paper,
we neglect the Eddington factor 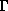 .
This approximation is valid as long as
.
This approximation is valid as long as
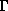 can be
regarded as a constant throughout the disc
and is much smaller than unity.
Both conditions hold well in Be-star discs.
Since the disc is considered to be optically thin for electron scattering,
the radial dependence of
can be
regarded as a constant throughout the disc
and is much smaller than unity.
Both conditions hold well in Be-star discs.
Since the disc is considered to be optically thin for electron scattering,
the radial dependence of 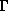 can be neglected.
Moreover, using the typical values for Be stars,
can be neglected.
Moreover, using the typical values for Be stars,
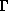 is as small as
is as small as
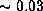 for a B0V star and
for a B0V star and 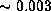 for a B5V star.
The radiative force is then written as
for a B5V star.
The radiative force is then written as
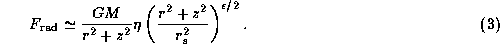
In the present model, the equation describing
the hydrostatic balance
in the vertical direction is written as
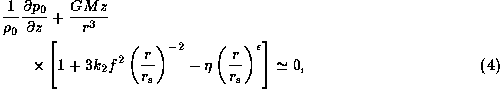
where 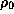 and
and 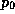 are the unperturbed density
and pressure, respectively.
Since the disc is isothermal, Eq.(4)
is integrated to give
the density distribution in the vertical direction:
are the unperturbed density
and pressure, respectively.
Since the disc is isothermal, Eq.(4)
is integrated to give
the density distribution in the vertical direction:
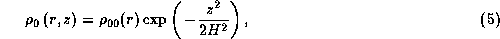
where  is the unperturbed density in the equatorial plane
and H the vertical scale-height of the disc given by
is the unperturbed density in the equatorial plane
and H the vertical scale-height of the disc given by
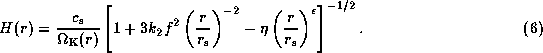
Here, 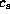 and
and 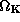 are
the isothermal sound speed and the Keplerian angular velocity,
respectively.
are
the isothermal sound speed and the Keplerian angular velocity,
respectively.
Since the density profiles of Be-star discs are
not well determined,
we adopt a simple power-law form for 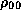 ,
,

where the index  is a constant.
Observationally, the density-gradient indices for Be stars
have been derived by a curve of growth method,
in which the disc is assumed to have
a constant opening angle and a density distribution
proportional to
is a constant.
Observationally, the density-gradient indices for Be stars
have been derived by a curve of growth method,
in which the disc is assumed to have
a constant opening angle and a density distribution
proportional to 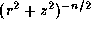 (e.g., Waters 1986).
The obtained value of n is different from star to star,
but is roughly in the range of
(e.g., Waters 1986).
The obtained value of n is different from star to star,
but is roughly in the range of 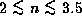 (Waters et al. 1987).
Considering the difference between a disc geometry assumed by
the curve of growth method
and the disc geometry adopted in this paper,
we infer the range of
(Waters et al. 1987).
Considering the difference between a disc geometry assumed by
the curve of growth method
and the disc geometry adopted in this paper,
we infer the range of  to be
to be 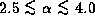 .
Theoretically,
.
Theoretically, 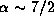 in the subsonic region
of the isothermal disc,
if the angular momentum distribution of the disc
is due to viscous stress
[see Eq. (11) of Lee et al. (1991)].
in the subsonic region
of the isothermal disc,
if the angular momentum distribution of the disc
is due to viscous stress
[see Eq. (11) of Lee et al. (1991)].
The radial distribution of the rotational angular velocity
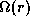 is derived
from the equation of motion in the radial direction
is derived
from the equation of motion in the radial direction
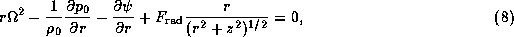
and is written explicitly in the form
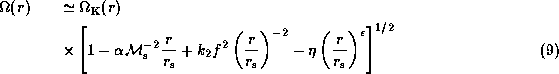
under the approximation 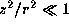 .
Here,
.
Here, 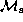 is the Mach number of disc rotation
at
is the Mach number of disc rotation
at 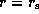 .
For typical Be stars,
.
For typical Be stars, 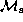 is given by
is given by
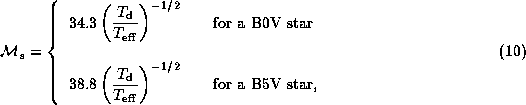
where we adopted
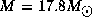 ,
, 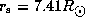 ,
and
,
and 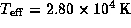 for a B0V star and
for a B0V star and
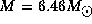 ,
, 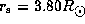 ,
and
,
and 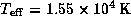 for a B5V star
(Allen 1973).
In the present model,
the epicyclic frequency
for a B5V star
(Allen 1973).
In the present model,
the epicyclic frequency 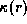 is given by
is given by
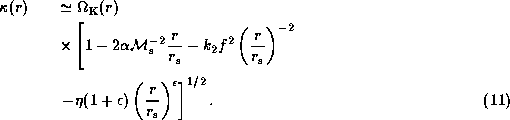
Note that the second, third, and fourth terms
between the square brackets in Eqs. (9) and (11)
denote the contributions from
the pressure gradient force in the disc,
the deviation from the point-mass potential due to
the rotational deformation of the star,
and the radiative force due to an ensemble of optically thin lines,
respectively.
The parameters which characterize the problem are
 ,
, 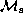 ,
, 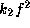 ,
, 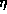 , and
, and  .
.



Next: 2.2 Equations for one-armed
Up: 2 The unperturbed disc
Previous: 2 The unperturbed disc
Atsuo Okazaki
平成9年3月15日 (土), 午後 1時19分3秒
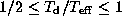 .
Here,
.
Here, 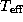 is the effective temperature of the star.
We also assume that the unperturbed disc is in hydrostatic equilibrium
in the vertical direction
and extends from the stellar surface (
is the effective temperature of the star.
We also assume that the unperturbed disc is in hydrostatic equilibrium
in the vertical direction
and extends from the stellar surface (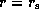 ) to infinity
in the radial direction.
We neglect radial advective motions and viscous effects.
The adopted value of the mean molecular weight is 0.6.
We use a cylindrical coordinate system
) to infinity
in the radial direction.
We neglect radial advective motions and viscous effects.
The adopted value of the mean molecular weight is 0.6.
We use a cylindrical coordinate system
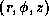 to describe the disc;
the origin is at the center of the star and
the z-axis is perpendicular to the disc midplane.
to describe the disc;
the origin is at the center of the star and
the z-axis is perpendicular to the disc midplane.
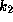 can be approximated as
can be approximated as
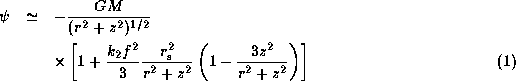
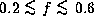 for B0-type Be stars
and
for B0-type Be stars
and 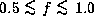 for B5-type Be stars.
The values of
for B5-type Be stars.
The values of 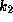 for rapidly rotating stars are not well known.
Theoretically,
for rapidly rotating stars are not well known.
Theoretically, 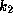 for non-rotating main-sequence stars has a
maximum value of
for non-rotating main-sequence stars has a
maximum value of 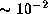 at a mass between 7 and
at a mass between 7 and 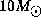 (Stothers 1974).
In general,
(Stothers 1974).
In general, 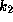 is a decreasing function of the degree of
the central condensation of the star:
The value of
is a decreasing function of the degree of
the central condensation of the star:
The value of 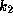 is smaller for a more evolved star
or for a star with larger uniform rotation
(Stothers 1974; Claret & Giménez 1993),
while it can be large for a star of which the inner part
rotates more rapidly than the outer part.
PSH adopted
is smaller for a more evolved star
or for a star with larger uniform rotation
(Stothers 1974; Claret & Giménez 1993),
while it can be large for a star of which the inner part
rotates more rapidly than the outer part.
PSH adopted 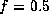 and
and
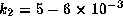 and SH studied the rotation effect
for
and SH studied the rotation effect
for 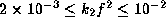 .
.
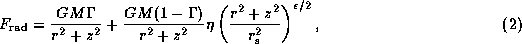
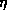 and
and  are parameters which characterize
the force due to an ensemble of optically thin lines.
According to Chen & Marlborough (1994),
are parameters which characterize
the force due to an ensemble of optically thin lines.
According to Chen & Marlborough (1994),
 should be a positive number which is much smaller than unity.
In the above expression,
should be a positive number which is much smaller than unity.
In the above expression,
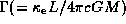 is the Eddington factor
that accounts for the reduction in the effective gravity
due to electron scattering.
Here,
is the Eddington factor
that accounts for the reduction in the effective gravity
due to electron scattering.
Here, 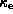 is the opacity due to electron scattering
per mass unit and L is the total luminosity of the star.
In the rest of this paper,
we neglect the Eddington factor
is the opacity due to electron scattering
per mass unit and L is the total luminosity of the star.
In the rest of this paper,
we neglect the Eddington factor 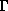 .
This approximation is valid as long as
.
This approximation is valid as long as
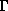 can be
regarded as a constant throughout the disc
and is much smaller than unity.
Both conditions hold well in Be-star discs.
Since the disc is considered to be optically thin for electron scattering,
the radial dependence of
can be
regarded as a constant throughout the disc
and is much smaller than unity.
Both conditions hold well in Be-star discs.
Since the disc is considered to be optically thin for electron scattering,
the radial dependence of 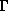 can be neglected.
Moreover, using the typical values for Be stars,
can be neglected.
Moreover, using the typical values for Be stars,
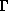 is as small as
is as small as
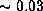 for a B0V star and
for a B0V star and 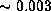 for a B5V star.
The radiative force is then written as
for a B5V star.
The radiative force is then written as
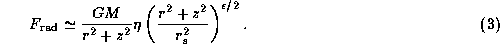
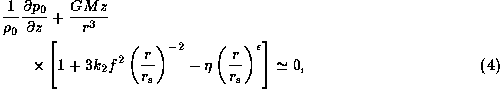
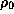 and
and 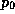 are the unperturbed density
and pressure, respectively.
Since the disc is isothermal, Eq.(
are the unperturbed density
and pressure, respectively.
Since the disc is isothermal, Eq.(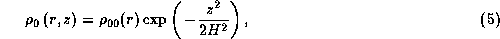
 is the unperturbed density in the equatorial plane
and H the vertical scale-height of the disc given by
is the unperturbed density in the equatorial plane
and H the vertical scale-height of the disc given by
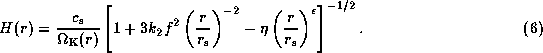
 and
and  are
the isothermal sound speed and the Keplerian angular velocity,
respectively.
are
the isothermal sound speed and the Keplerian angular velocity,
respectively.
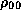 ,
,

 is a constant.
Observationally, the density-gradient indices for Be stars
have been derived by a curve of growth method,
in which the disc is assumed to have
a constant opening angle and a density distribution
proportional to
is a constant.
Observationally, the density-gradient indices for Be stars
have been derived by a curve of growth method,
in which the disc is assumed to have
a constant opening angle and a density distribution
proportional to 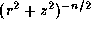 (e.g., Waters 1986).
The obtained value of n is different from star to star,
but is roughly in the range of
(e.g., Waters 1986).
The obtained value of n is different from star to star,
but is roughly in the range of 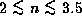 (Waters et al. 1987).
Considering the difference between a disc geometry assumed by
the curve of growth method
and the disc geometry adopted in this paper,
we infer the range of
(Waters et al. 1987).
Considering the difference between a disc geometry assumed by
the curve of growth method
and the disc geometry adopted in this paper,
we infer the range of  to be
to be 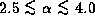 .
Theoretically,
.
Theoretically, 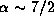 in the subsonic region
of the isothermal disc,
if the angular momentum distribution of the disc
is due to viscous stress
[see Eq. (11) of Lee et al. (1991)].
in the subsonic region
of the isothermal disc,
if the angular momentum distribution of the disc
is due to viscous stress
[see Eq. (11) of Lee et al. (1991)].
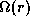 is derived
from the equation of motion in the radial direction
is derived
from the equation of motion in the radial direction
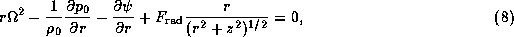
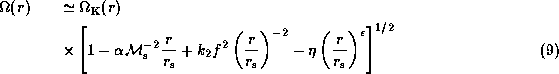
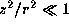 .
Here,
.
Here, 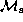 is the Mach number of disc rotation
at
is the Mach number of disc rotation
at 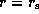 .
For typical Be stars,
.
For typical Be stars, 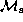 is given by
is given by
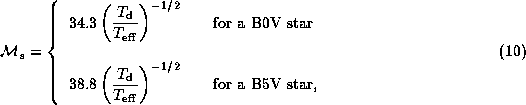
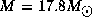 ,
, 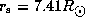 ,
and
,
and 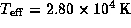 for a B0V star and
for a B0V star and
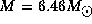 ,
, 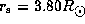 ,
and
,
and 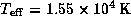 for a B5V star
(Allen 1973).
In the present model,
the epicyclic frequency
for a B5V star
(Allen 1973).
In the present model,
the epicyclic frequency 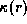 is given by
is given by
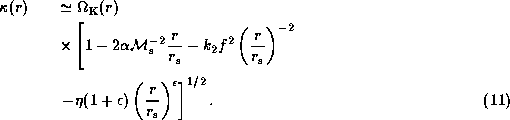
 ,
, 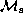 ,
, 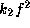 ,
, 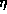 , and
, and  .
.