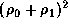We consider only Balmer lines,
which are assumed to be emitted from the entire disk.
Neither the radiation from the central star nor the continuum radiation
from the disk are included.
In the Balmer-line regions of Be-star disks,
hydrogen is almost fully ionized and
electrons populate in accordance with an incomplete Rosseland cycle
(i.e., the photoionization from the second energy level of
hydrogen atoms
followed by the recombination and the subsequent cascade transitions).
Hence, we assume that the population density of
the second energy level n
is proportional to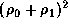 
, i.e.,
where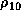 
is the Eulerian perturbation of the density
on the equatorial plane, and
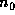is the unperturbed population density, given by
We take into account only the thermal broadening
as the line-broadening mechanism.
The line-absorption coefficient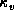 
at a line-of-sight velocity v is then expressed as
where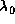 
is the rest wavelength, f the absorption oscillator
strength of the transition, and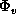 
the local absorption profile,
given by
Here,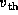 
is the thermal velocity of hydrogen and
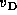is the line-of-sight velocity.
In the present model,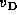 
is given by
where i is the inclination angle between the observer's line-of-sight
and the direction normal to the equatorial plane.
Since the disk is geometrically thin,
the last term on the right-hand side in equation (15),
i.e., the line-of-sight component of the vertical velocity perturbation,
is negligible unless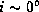 
.
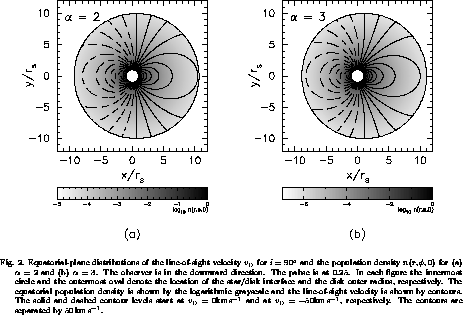
Figure 2 shows the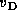 
and
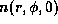distributions for 
.
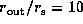Figure 2a is for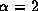 
and figure 2b for 
.
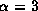The value of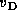 
is calculated for 
.
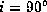The observer is in the downward direction on the figure.
The phase of the variations is 0.25.
(We choose phase 0 to be the phase at which the peak of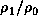 
locates in front of the star.
Hence, the profile asymmetry is largest at phases 0.25 and 0.75.)
In each figure the innermost circle and the outermost oval
denote the location of
the star/disk interface and the disk outer radius, respectively.
The distribution of the equatorial population density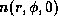 
is indicated by the logarithmic grayscale,
and the line-of-sight velocity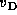 
is shown by contours.
The solid and dashed contour levels start at
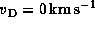and at 
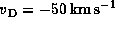, respectively.
The contours are separated by 
.
In figure 2 we notice that the perturbed disk becomes eccentric due to the fundamental m=1 mode, and that, except for the innermost part of the disk, the velocity field associated with the perturbation points toward the observer. These features imply that optically-thick line profiles from disks perturbed by the one-armed fundamental modes vary in a manner in which the profile as a whole shifts blueward (redward) when the red (violet) peak is stronger.
The optical depths of the lines are often used to discuss
the profiles.
Hence, in order to characterize the population density
of the unperturbed disk,
we introduce the characteristic optical depth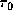 
defined by
We can then express the absorption coefficient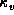 
as
We compute the emission line profiles by integrating
the surface intensities along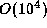 
parallel rays
penetrating the disk under the inclination angle i.
The rays are more concentrated towards
the higher-density, more rapidly rotating region around the star.
For simplicity, we assume that the source function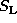 
is constant over the entire disk region.
Then, the surface intensity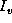 
along each ray is
simply reduced to
where the optical depth along the ray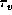 
is given by
Here, ds is the line element along the ray.
We evaluated the line integral in equation (19)
using the values of
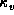on the 
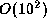depth steps along the ray.
In these calculations we adopted a somewhat crude velocity resolution
of 
in order to reduce the computing time.
In subsequent sections we also present profiles of optically-thin
emission lines for the sake of a comparison with
optically-thick line profiles.
To obtain the optically-thin profiles,
we adopted a method slightly different from that described above.
The method using a bundle of rays is not adequate
for calculating the optically-thin lines.
It needs too many rays, each of which
must have a large number of depth steps
for computing the optically-thin line profiles with
a sufficient accuracy.
Hence, instead of calculating the surface intensities along rays,
we integrated the line absorption coefficient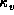 
given by equation (13)
over the entire volume of the disk,
because 
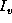in equation (18) is
approximated to be proportional to
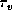for the optically-thin lines.
