


Next: 5 Variations of Line
Up: Abstract
Previous: 3 Methods for Computing
In this and subsequent sections
we present the numerical results obtained by
the method described in the previous section.
We computed line profiles for
disk sizes of 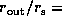 5, 10, and 20,
density-gradient indices of
5, 10, and 20,
density-gradient indices of  1, 2, 3, and 4,
characteristic optical depths of
1, 2, 3, and 4,
characteristic optical depths of 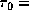
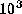 ,
, 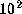 , and 10
and an optically thin case,
and inclination angles of i =
, and 10
and an optically thin case,
and inclination angles of i = 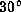 ,
, 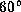 , and
, and 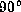 .
Note that observed H
.
Note that observed H emission arises, on the average,
in the
emission arises, on the average,
in the 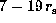 range (Slettebak et al. 1992).
range (Slettebak et al. 1992).
Here, we comment on the range of 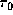 estimated for
the disks of actual Be stars.
For shell (
estimated for
the disks of actual Be stars.
For shell (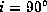 ) stars,
the optical depths of the envelopes are
determined by the central depth analysis of
the observed shell absorption lines (e.g., Kogure et al. 1978).
Kogure (1990) collected the results obtained
for some shell stars,
and concluded that the optical depths in H
) stars,
the optical depths of the envelopes are
determined by the central depth analysis of
the observed shell absorption lines (e.g., Kogure et al. 1978).
Kogure (1990) collected the results obtained
for some shell stars,
and concluded that the optical depths in H lines
lines 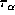 range from 2000 to 5000 for fully-developed shell stars,
while
range from 2000 to 5000 for fully-developed shell stars,
while 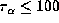 for weak shell stars.
On the other hand, we can estimate
for weak shell stars.
On the other hand, we can estimate 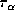 for
for 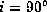 in our model as
in our model as
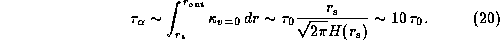
Hence, we found that
disks of the actual Be stars are characterized
by 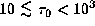 .
.
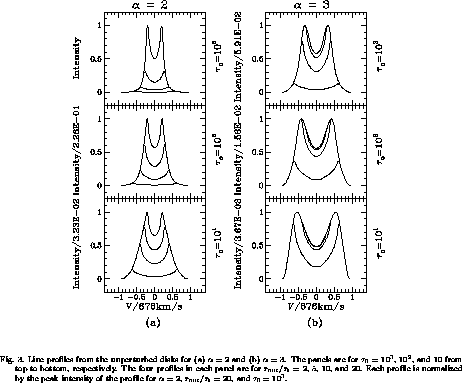
Figure 3 shows the various line profiles from the unperturbed disks
for 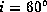 .
The left panels are for
.
The left panels are for 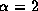 and
the right panels for
and
the right panels for 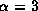 .
The panels are for
.
The panels are for 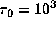 ,
, 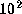 , and 10
from top to bottom, respectively.
In each panel we show profiles for four outer disk radii:
, and 10
from top to bottom, respectively.
In each panel we show profiles for four outer disk radii:
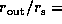 2, 5, 10, and 20.
Each profile is normalized by the peak intensity
of the unperturbed profile from the disk with
2, 5, 10, and 20.
Each profile is normalized by the peak intensity
of the unperturbed profile from the disk with 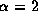 ,
,
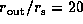 , and
, and 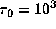 .
Except for the line widths,
the profiles for
.
Except for the line widths,
the profiles for 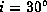 and
and 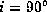 are
roughly the same as those shown in figure 3.
are
roughly the same as those shown in figure 3.
We now consider the effects of the density gradient index  and the optical depth
and the optical depth 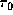 on the line profiles.
As demonstrated by Horne and Marsh (1986),
the intensities along the line-of-sights
through the high-density region saturate in optically-thick cases.
Hence, the area under the saturated line intensity
increases with increasing characteristic optical depth
on the line profiles.
As demonstrated by Horne and Marsh (1986),
the intensities along the line-of-sights
through the high-density region saturate in optically-thick cases.
Hence, the area under the saturated line intensity
increases with increasing characteristic optical depth 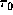 .
Simultaneously, the unsaturated intensities from an outer region
of the disk increases with
.
Simultaneously, the unsaturated intensities from an outer region
of the disk increases with 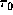 .
As a result, the contribution of the outer region of the disk
monotonically increases with
.
As a result, the contribution of the outer region of the disk
monotonically increases with 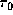 .
.
On the other hand, the velocities of the violet and red
peaks for 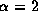 are independent of
are independent of 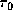 , and
are given by
, and
are given by 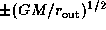 ,
while those for
,
while those for 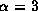 decrease towards
decrease towards
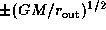 as
as 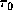 increases.
This feature can be understood as follows:
The emission in each velocity bin arises from a different
crescent-shaped region of the disk surface
[see figure 2 and also figure 1 of Horne and Marsh (1986)].
For
increases.
This feature can be understood as follows:
The emission in each velocity bin arises from a different
crescent-shaped region of the disk surface
[see figure 2 and also figure 1 of Horne and Marsh (1986)].
For 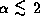 , the strongest emission arises,
irrespective of
, the strongest emission arises,
irrespective of 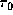 , from the crescent-shaped region
tangent to the outer radius of the disk.
For
, from the crescent-shaped region
tangent to the outer radius of the disk.
For 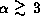 , however,
it arises from the crescent-shaped region
tangent to the radius where the optical depths
along the line-of-sights are almost unity.
This radius increases with increasing
, however,
it arises from the crescent-shaped region
tangent to the radius where the optical depths
along the line-of-sights are almost unity.
This radius increases with increasing 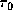 .
Thus, for
.
Thus, for 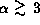 ,
the peak velocity is a measure for a radius
within which most of the emission arises.
,
the peak velocity is a measure for a radius
within which most of the emission arises.



Next: 5 Variations of Line
Up: Abstract
Previous: 3 Methods for Computing
Atsuo Okazaki
平成9年1月6日 (月), 午後 6時16分22秒
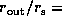 5, 10, and 20,
density-gradient indices of
5, 10, and 20,
density-gradient indices of  1, 2, 3, and 4,
characteristic optical depths of
1, 2, 3, and 4,
characteristic optical depths of 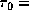
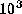 ,
, 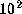 , and 10
and an optically thin case,
and inclination angles of i =
, and 10
and an optically thin case,
and inclination angles of i = 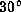 ,
, 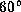 , and
, and 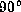 .
Note that observed H
.
Note that observed H emission arises, on the average,
in the
emission arises, on the average,
in the 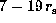 range (Slettebak et al. 1992).
range (Slettebak et al. 1992).
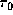 estimated for
the disks of actual Be stars.
For shell (
estimated for
the disks of actual Be stars.
For shell (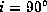 ) stars,
the optical depths of the envelopes are
determined by the central depth analysis of
the observed shell absorption lines (e.g., Kogure et al. 1978).
Kogure (1990) collected the results obtained
for some shell stars,
and concluded that the optical depths in H
) stars,
the optical depths of the envelopes are
determined by the central depth analysis of
the observed shell absorption lines (e.g., Kogure et al. 1978).
Kogure (1990) collected the results obtained
for some shell stars,
and concluded that the optical depths in H lines
lines 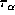 range from 2000 to 5000 for fully-developed shell stars,
while
range from 2000 to 5000 for fully-developed shell stars,
while 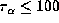 for weak shell stars.
On the other hand, we can estimate
for weak shell stars.
On the other hand, we can estimate 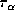 for
for 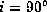 in our model as
in our model as
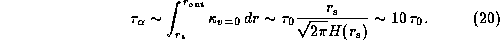
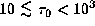 .
.

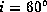 .
The left panels are for
.
The left panels are for 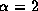 and
the right panels for
and
the right panels for 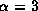 .
The panels are for
.
The panels are for 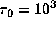 ,
, 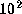 , and 10
from top to bottom, respectively.
In each panel we show profiles for four outer disk radii:
, and 10
from top to bottom, respectively.
In each panel we show profiles for four outer disk radii:
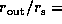 2, 5, 10, and 20.
Each profile is normalized by the peak intensity
of the unperturbed profile from the disk with
2, 5, 10, and 20.
Each profile is normalized by the peak intensity
of the unperturbed profile from the disk with 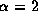 ,
,
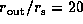 , and
, and 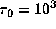 .
Except for the line widths,
the profiles for
.
Except for the line widths,
the profiles for 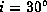 and
and 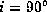 are
roughly the same as those shown in figure 3.
are
roughly the same as those shown in figure 3.
 and the optical depth
and the optical depth 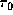 on the line profiles.
As demonstrated by Horne and Marsh (1986),
the intensities along the line-of-sights
through the high-density region saturate in optically-thick cases.
Hence, the area under the saturated line intensity
increases with increasing characteristic optical depth
on the line profiles.
As demonstrated by Horne and Marsh (1986),
the intensities along the line-of-sights
through the high-density region saturate in optically-thick cases.
Hence, the area under the saturated line intensity
increases with increasing characteristic optical depth 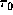 .
Simultaneously, the unsaturated intensities from an outer region
of the disk increases with
.
Simultaneously, the unsaturated intensities from an outer region
of the disk increases with 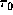 .
As a result, the contribution of the outer region of the disk
monotonically increases with
.
As a result, the contribution of the outer region of the disk
monotonically increases with 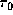 .
.
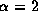 are independent of
are independent of 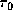 , and
are given by
, and
are given by 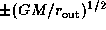 ,
while those for
,
while those for 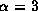 decrease towards
decrease towards
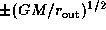 as
as 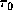 increases.
This feature can be understood as follows:
The emission in each velocity bin arises from a different
crescent-shaped region of the disk surface
[see figure 2 and also figure 1 of Horne and Marsh (1986)].
For
increases.
This feature can be understood as follows:
The emission in each velocity bin arises from a different
crescent-shaped region of the disk surface
[see figure 2 and also figure 1 of Horne and Marsh (1986)].
For 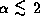 , the strongest emission arises,
irrespective of
, the strongest emission arises,
irrespective of 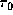 , from the crescent-shaped region
tangent to the outer radius of the disk.
For
, from the crescent-shaped region
tangent to the outer radius of the disk.
For 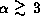 , however,
it arises from the crescent-shaped region
tangent to the radius where the optical depths
along the line-of-sights are almost unity.
This radius increases with increasing
, however,
it arises from the crescent-shaped region
tangent to the radius where the optical depths
along the line-of-sights are almost unity.
This radius increases with increasing 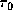 .
Thus, for
.
Thus, for 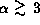 ,
the peak velocity is a measure for a radius
within which most of the emission arises.
,
the peak velocity is a measure for a radius
within which most of the emission arises.