


Next: Growth of the Eccentric
Up: summary
Previous: Truncation Radius
Fig. 3 shows (a) the evolution of the disc mass 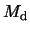 and the mass capture rate by the neutron star,
and the mass capture rate by the neutron star,
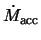 ,
over
,
over
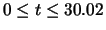 and
(b) their orbital-phase dependence over
and
(b) their orbital-phase dependence over
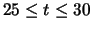 ,
where the unit of time is
,
where the unit of time is 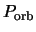 .
Here,
.
Here, 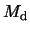 is defined as the mass in
is defined as the mass in
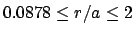 and
and
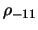 is the base density of the
disc normalized by
is the base density of the
disc normalized by
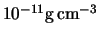 .
In Fig. 3(b), the horizontal line denotes the averaged
mass capture rate by the neutron star.
On average, the neutron star captures the disc mass at the rate
of
.
In Fig. 3(b), the horizontal line denotes the averaged
mass capture rate by the neutron star.
On average, the neutron star captures the disc mass at the rate
of
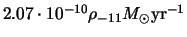 ,
which will produce
,
which will produce
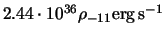 of luminosity if all the material accretes
on to the neutron star.
of luminosity if all the material accretes
on to the neutron star.
Figure 3:
(a) Evolution of the disc mass and
the mass capture rate by the neutron star and
(b) their orbital-phase dependence.
In panel (b), averaging is done over
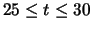 ,
where the unit of time is
,
where the unit of time is  .
In each panel, the blue line denotes the mass capture rate
.
In each panel, the blue line denotes the mass capture rate
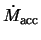 ,
while the red line denotes the disc mass
,
while the red line denotes the disc mass 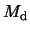 ,
which is defined by the mass in
,
which is defined by the mass in
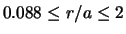 .
The horizontal dashed line in panel (b) denotes the mass capture r
ate
averaged over one orbital period.
.
The horizontal dashed line in panel (b) denotes the mass capture r
ate
averaged over one orbital period.
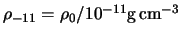 ,
where
,
where 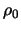 is the base density of the disc.
is the base density of the disc.
|
|



Next: Growth of the Eccentric
Up: summary
Previous: Truncation Radius
Atsuo Okazaki
2002-01-28
![]() and the mass capture rate by the neutron star,
and the mass capture rate by the neutron star,
![]() ,
over
,
over
![]() and
(b) their orbital-phase dependence over
and
(b) their orbital-phase dependence over
![]() ,
where the unit of time is
,
where the unit of time is ![]() .
Here,
.
Here, ![]() is defined as the mass in
is defined as the mass in
![]() and
and
![]() is the base density of the
disc normalized by
is the base density of the
disc normalized by
![]() .
In Fig. 3(b), the horizontal line denotes the averaged
mass capture rate by the neutron star.
On average, the neutron star captures the disc mass at the rate
of
.
In Fig. 3(b), the horizontal line denotes the averaged
mass capture rate by the neutron star.
On average, the neutron star captures the disc mass at the rate
of
![]() ,
which will produce
,
which will produce
![]() of luminosity if all the material accretes
on to the neutron star.
of luminosity if all the material accretes
on to the neutron star.
![\includegraphics[width=9cm]{mdot_cgs.ps}](img71.gif)