


Next: Evolution of Disc Mass
Up: summary
Previous: Disc Structure
To determine the location of the truncation radius,
a non-linear least square fitting method
for the radial distribution of
the surface density 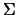 is applied.
The fitting function adopted is
is applied.
The fitting function adopted is
where 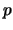 and
and  are constants and
are constants and
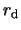 is the truncation radius.
is the truncation radius.
Fig. 2 shows (a) the evolution of the disc radius over
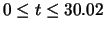 and
(b) the dependence of the disc radius on the orbital phase over
and
(b) the dependence of the disc radius on the orbital phase over
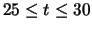 ,
where the unit of time is
,
where the unit of time is 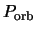 .
The mean value of
.
The mean value of 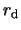 averaged over
averaged over
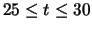 is
is
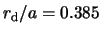 .
.
Figure 2:
(a) Evolution of the radius of the truncated disc,
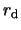 .
The blue dot denotes
.
The blue dot denotes 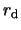 at each instance.
The horizontal lines denote the 2:1, the 3:1, the 4:1,
at each instance.
The horizontal lines denote the 2:1, the 3:1, the 4:1,  ,
and the 15:1 resonance radii from top to bottom.
The red line denotes the orbit of the neutron star.
The periastron passage of the neutron star is denoted
by vertical dashed lines.
(b) Orbital-phase dependence of the trncation radius.
Averaging is done over
,
and the 15:1 resonance radii from top to bottom.
The red line denotes the orbit of the neutron star.
The periastron passage of the neutron star is denoted
by vertical dashed lines.
(b) Orbital-phase dependence of the trncation radius.
Averaging is done over
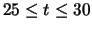 in units of
in units of  .
The periastron passage of the neutron star occurs at pahse 0.
The mean value of
.
The periastron passage of the neutron star occurs at pahse 0.
The mean value of 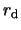 over this period is
over this period is
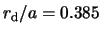 .
.
|
|



Next: Evolution of Disc Mass
Up: summary
Previous: Disc Structure
Atsuo Okazaki
2002-01-28
![]() is applied.
The fitting function adopted is
is applied.
The fitting function adopted is
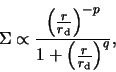
![]() and
(b) the dependence of the disc radius on the orbital phase over
and
(b) the dependence of the disc radius on the orbital phase over
![]() ,
where the unit of time is
,
where the unit of time is ![]() .
The mean value of
.
The mean value of ![]() averaged over
averaged over
![]() is
is
![]() .
.
![\includegraphics[width=9cm]{diskrad.ps}](img62.gif)