


Next: Precession of the Eccentric
Up: summary
Previous: Evolution of Disc Mass
We study the evolution of the eccentricity
of the Be disc by decomposing the surface
density distribution into Fourier components
which vary as
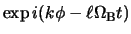 ,
where
,
where 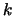 and
and 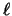 are the azimuthal and time-harmonic numbers,
respectively, and
are the azimuthal and time-harmonic numbers,
respectively, and
![$\Omega_{\rm B} = [G(M_{*}+M_x)/a^3]^{1/2}$](img78.gif) is the frequency of mean binary rotation with semimajor axis
is the frequency of mean binary rotation with semimajor axis 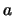 .
.
As in Lubow (1991), we define the mode strength
where 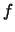 and
and 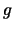 are either
are either 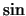 or
or 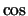 functions,
functions, 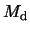 is the disc mass, and
is the disc mass, and 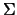 is the surface density of the disc.
For reducing computing time, we compute the surface density
by summing up
is the surface density of the disc.
For reducing computing time, we compute the surface density
by summing up 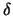 functioins at particle positions.
Then, the total strength of the mode
functioins at particle positions.
Then, the total strength of the mode 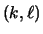 is defined by
is defined by
Fig. 4 shows the strengths of several modes.
The growth rate of the (1,0) mode (i.e., eccentric mode) averag
ed
over 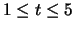 is
is
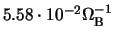 .
.
Figure 4:
Strengths of several modes.
The solid, the dashed, the dash-dotted, and
the dotted lines denote the strengths of
the (1,0) mode, the (2,3) mode, the (1,1) mode,
and the (2,2) mode, respectively.
|
|



Next: Precession of the Eccentric
Up: summary
Previous: Evolution of Disc Mass
Atsuo Okazaki
2002-01-28
![]() ,
where
,
where ![]() and
and ![]() are the azimuthal and time-harmonic numbers,
respectively, and
are the azimuthal and time-harmonic numbers,
respectively, and
![]() is the frequency of mean binary rotation with semimajor axis
is the frequency of mean binary rotation with semimajor axis ![]() .
.
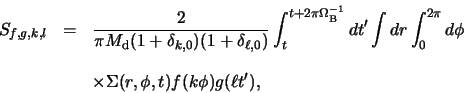
![]() is
is
![]() .
.
![\includegraphics[width=9cm]{modes.ps}](img90.gif)