


Next: Truncation Radius
Up: summary
Previous: Parameters
Fig. 1 shows the evolution of surface density (left pan
el) and
the final disc structure (right panel).
Averaging is done by using
where 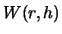 is the kernel given by
is the kernel given by
Figure 1:
(Left) Surface density evolution from 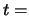 0 to 30
in units of
0 to 30
in units of  .
The interval of time between adjacent contours
is 5
(
.
The interval of time between adjacent contours
is 5
(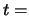 0, 5,
0, 5,  from bottom).
(Right) Disc structure at
from bottom).
(Right) Disc structure at 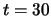 .
The black, the blue, and the red lines are for
the surface density, the radial Mach number,
and the angular velocity
normalized by the stellar break-up velocity, respectively.
The magenta line is for
.
The black, the blue, and the red lines are for
the surface density, the radial Mach number,
and the angular velocity
normalized by the stellar break-up velocity, respectively.
The magenta line is for
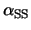 and the green line is for
the smoothing length normalized by
the disc scale-height.
and the green line is for
the smoothing length normalized by
the disc scale-height.
![\includegraphics[height=10cm]{rdist.ps}](img56.gif) |
Atsuo Okazaki
2002-01-28
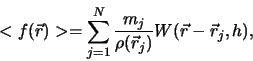
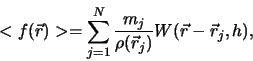
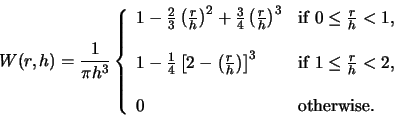
![\includegraphics[height=10cm]{rdist.ps}](img56.gif)