


Next: Characteristics of warping
Up: No Title
Previous: Introduction
We take a non-self-gravitating, axisymmetric
disc as an unperturbed equilibrium disc.
It rotates around a black hole of
mass 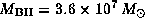 ,
of which the Schwarzschild radius
,
of which the Schwarzschild radius
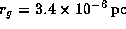 .
To simulate the weak general relativistic effect,
we use the pseudo-Newtonian potential (Paczynski & Wiita 1980).
We assume that the geometrically-thin maser disc is
in hydrostatic equilibrium in the vertical
direction, and has an inner radius,
.
To simulate the weak general relativistic effect,
we use the pseudo-Newtonian potential (Paczynski & Wiita 1980).
We assume that the geometrically-thin maser disc is
in hydrostatic equilibrium in the vertical
direction, and has an inner radius, 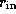 ,
and an outer radius,
,
and an outer radius, 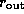 .
We neglect radial advective motions and viscous effects.
We use cylindrical coordinates
.
We neglect radial advective motions and viscous effects.
We use cylindrical coordinates 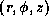 ;
the z-axis is normal to the disc midplane
and is not the vertical axis of the galaxy.
;
the z-axis is normal to the disc midplane
and is not the vertical axis of the galaxy.
We assume that the gas
obeys a polytropic relation with index 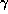 .
The unperturbed density distribution is then given by
.
The unperturbed density distribution is then given by
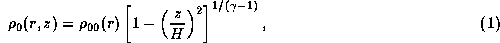
where 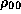 is the unperturbed density in the equatorial plane,
and H the half-thickness of the disc given by
is the unperturbed density in the equatorial plane,
and H the half-thickness of the disc given by
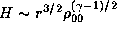 .
In our model, we are free to specify a functional form of
.
In our model, we are free to specify a functional form of  .
For simplicity, we adopt a toy model for
.
For simplicity, we adopt a toy model for  ,
,
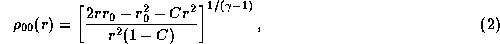
where 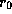 is the radius at which the density reaches its maximum
[
is the radius at which the density reaches its maximum
[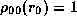 ],
and C a constant defined by
],
and C a constant defined by
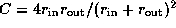 .
This density distribution was used by Miyama et al. (1994)
to study the stability of circumstellar discs.
.
This density distribution was used by Miyama et al. (1994)
to study the stability of circumstellar discs.
Since global features of the eigenmodes are not sensitive to
the values of 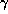 , C, and
, C, and 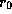 ,
we adopt a particular density distribution
such that
,
we adopt a particular density distribution
such that 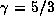 ,
, 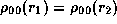 ,
and
,
and 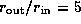 .
Here,
.
Here, 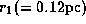 and
and 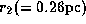 are, respectively,
the inner and outer radii of the region from which
the maser emission arises.
For this particular choice of parameters,
are, respectively,
the inner and outer radii of the region from which
the maser emission arises.
For this particular choice of parameters,
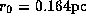 ,
, 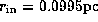 ,
and
,
and 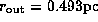 .
.
We normalize H such that the maximum half-thickness of
the region in which 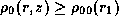 becomes
becomes 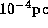 (hereafter, we refer to this region as the maser emission region).
Figure 1 shows the density distribution
in the unperturbed disc by contours.
In Fig. 1,
the dashed line denotes the maser emission region.
(hereafter, we refer to this region as the maser emission region).
Figure 1 shows the density distribution
in the unperturbed disc by contours.
In Fig. 1,
the dashed line denotes the maser emission region.
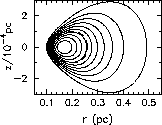
Figure 1: Density distribution in
the unperturbed disc.
The dashed line denotes the maser emission region,
in which 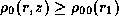 .
The contours are separated by 0.1
.
The contours are separated by 0.1
We consider a linear, adiabatic m=1 perturbation superposed on
the unperturbed disc.
The perturbation varies as 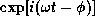 ,
where
,
where  is the frequency of the perturbation.
After some manipulations,
we finally have the following equation describing the linear,
adiabatic m=1 perturbation:
is the frequency of the perturbation.
After some manipulations,
we finally have the following equation describing the linear,
adiabatic m=1 perturbation:
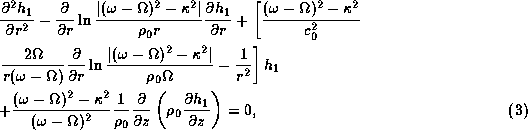
where 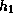 is the enthalpy perturbation
defined by
is the enthalpy perturbation
defined by 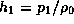 ,
,
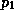 the Eulerian perturbation of the pressure,
the Eulerian perturbation of the pressure,
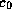 the sound speed in the unperturbed disc,
and
the sound speed in the unperturbed disc,
and 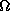 and
and  the angular frequency of disc rotation and
the epicyclic frequency, respectively.
the angular frequency of disc rotation and
the epicyclic frequency, respectively.
As the boundary conditions for Eq. (3),
we require that
the Lagrangian perturbation to the pressure
vanishes on the disc surface
and 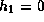 in the equatorial plane.
The latter condition is for warping modes.
We solve Eq. (3)
in the
in the equatorial plane.
The latter condition is for warping modes.
We solve Eq. (3)
in the 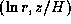 -plane
with 101 grid points in the radial direction and
51 grid points in the vertical direction.
To avoid singularities, we pose the inner and outer boundaries
of the computational domain at
-plane
with 101 grid points in the radial direction and
51 grid points in the vertical direction.
To avoid singularities, we pose the inner and outer boundaries
of the computational domain at 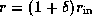 and
and 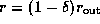 with
with 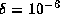 , respectively.
We have verified that the value of
, respectively.
We have verified that the value of 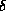 does not affect
the global features of the eigenmodes
as long as
does not affect
the global features of the eigenmodes
as long as  .
.



Next: Characteristics of warping
Up: No Title
Previous: Introduction
Atsuo Okazaki
平成8年12月20日 (金), 午後 3時14分19秒
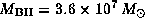 ,
of which the Schwarzschild radius
,
of which the Schwarzschild radius
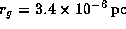 .
To simulate the weak general relativistic effect,
we use the pseudo-Newtonian potential (Paczynski & Wiita 1980).
We assume that the geometrically-thin maser disc is
in hydrostatic equilibrium in the vertical
direction, and has an inner radius,
.
To simulate the weak general relativistic effect,
we use the pseudo-Newtonian potential (Paczynski & Wiita 1980).
We assume that the geometrically-thin maser disc is
in hydrostatic equilibrium in the vertical
direction, and has an inner radius, 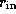 ,
and an outer radius,
,
and an outer radius, 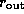 .
We neglect radial advective motions and viscous effects.
We use cylindrical coordinates
.
We neglect radial advective motions and viscous effects.
We use cylindrical coordinates 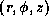 ;
the z-axis is normal to the disc midplane
and is not the vertical axis of the galaxy.
;
the z-axis is normal to the disc midplane
and is not the vertical axis of the galaxy.
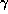 .
The unperturbed density distribution is then given by
.
The unperturbed density distribution is then given by
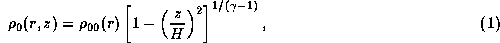
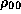 is the unperturbed density in the equatorial plane,
and H the half-thickness of the disc given by
is the unperturbed density in the equatorial plane,
and H the half-thickness of the disc given by
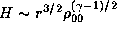 .
In our model, we are free to specify a functional form of
.
In our model, we are free to specify a functional form of 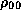 .
For simplicity, we adopt a toy model for
.
For simplicity, we adopt a toy model for 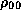 ,
,
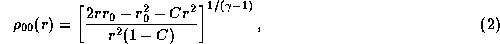
 is the radius at which the density reaches its maximum
[
is the radius at which the density reaches its maximum
[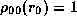 ],
and C a constant defined by
],
and C a constant defined by
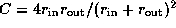 .
This density distribution was used by Miyama et al. (1994)
to study the stability of circumstellar discs.
.
This density distribution was used by Miyama et al. (1994)
to study the stability of circumstellar discs.
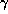 , C, and
, C, and 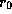 ,
we adopt a particular density distribution
such that
,
we adopt a particular density distribution
such that 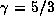 ,
, 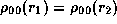 ,
and
,
and 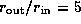 .
Here,
.
Here, 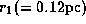 and
and 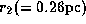 are, respectively,
the inner and outer radii of the region from which
the maser emission arises.
For this particular choice of parameters,
are, respectively,
the inner and outer radii of the region from which
the maser emission arises.
For this particular choice of parameters,
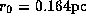 ,
, 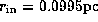 ,
and
,
and 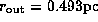 .
.
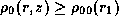 becomes
becomes 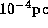 (hereafter, we refer to this region as the maser emission region).
Figure
(hereafter, we refer to this region as the maser emission region).
Figure 
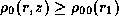 .
The contours are separated by 0.1
.
The contours are separated by 0.1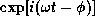 ,
where
,
where  is the frequency of the perturbation.
After some manipulations,
we finally have the following equation describing the linear,
adiabatic m=1 perturbation:
is the frequency of the perturbation.
After some manipulations,
we finally have the following equation describing the linear,
adiabatic m=1 perturbation:
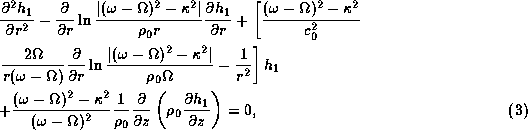
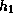 is the enthalpy perturbation
defined by
is the enthalpy perturbation
defined by 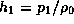 ,
,
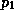 the Eulerian perturbation of the pressure,
the Eulerian perturbation of the pressure,
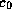 the sound speed in the unperturbed disc,
and
the sound speed in the unperturbed disc,
and 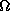 and
and  the angular frequency of disc rotation and
the epicyclic frequency, respectively.
the angular frequency of disc rotation and
the epicyclic frequency, respectively.
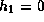 in the equatorial plane.
The latter condition is for warping modes.
We solve Eq. (
in the equatorial plane.
The latter condition is for warping modes.
We solve Eq. (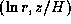 -plane
with 101 grid points in the radial direction and
51 grid points in the vertical direction.
To avoid singularities, we pose the inner and outer boundaries
of the computational domain at
-plane
with 101 grid points in the radial direction and
51 grid points in the vertical direction.
To avoid singularities, we pose the inner and outer boundaries
of the computational domain at 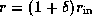 and
and 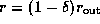 with
with 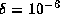 , respectively.
We have verified that the value of
, respectively.
We have verified that the value of 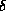 does not affect
the global features of the eigenmodes
as long as
does not affect
the global features of the eigenmodes
as long as  .
.