


Next: 2.2 m=1 Perturbation Patterns
Up: 2 m=1 Perturbation Patterns
Previous: 2 m=1 Perturbation Patterns
We assume that an unperturbed disk is steady, axisymmetric,
and nearly Keplerian.
For simplicity, the disk was assumed to be isothermal;
the disk temperature adopted
was 2/3 of the effective temperature of the central star.
In addition, we assumed that the disk extends from the surface of
the central star (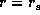 ) to
the outer radius (
) to
the outer radius (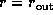 ).
The adopted value of the mean molecular weight was 0.6.
We took a B0 main-sequence star as being a typical central star,
because many Be stars exhibiting long-term V/R variations are
early B stars (Hirata, Hubert-Delplace 1981).
The quantities characterizing the central star were from Allen (1973)
(see table 1 of Paper I).
).
The adopted value of the mean molecular weight was 0.6.
We took a B0 main-sequence star as being a typical central star,
because many Be stars exhibiting long-term V/R variations are
early B stars (Hirata, Hubert-Delplace 1981).
The quantities characterizing the central star were from Allen (1973)
(see table 1 of Paper I).
We used a cylindrical coordinate system
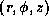 to describe the disk;
the origin is at the center of the star and
the z-axis is perpendicular to the disk midplane.
For convenience's sake, we assume in later sections that
the projection of the observer's direction onto the equatorial plane
is at
to describe the disk;
the origin is at the center of the star and
the z-axis is perpendicular to the disk midplane.
For convenience's sake, we assume in later sections that
the projection of the observer's direction onto the equatorial plane
is at 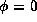 .
.
From the equation describing the hydrostatic balance of the disk in
the vertical direction,
we obtain the density distribution in the vertical direction,
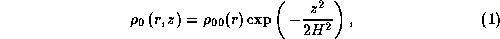
where 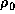 is the unperturbed density,
is the unperturbed density,
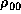 is the unperturbed density on the equatorial plane,
and H is the vertical scale-height of the disk, given by
is the unperturbed density on the equatorial plane,
and H is the vertical scale-height of the disk, given by
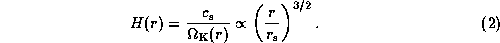
Here, 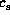 and
and 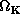 are
the isothermal sound speed and the Keplerian angular frequency,
respectively.
are
the isothermal sound speed and the Keplerian angular frequency,
respectively.
At present, the density profiles of the Be-star disks are
not well determined observationally.
Hence, we adopt a simple power-law form for 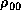 ,
,
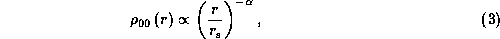
where the index  is a constant.
The surface density is then proportional to
is a constant.
The surface density is then proportional to 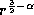 .
.
In the present model, the angular frequency of disk rotation
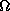 and
the epicyclic frequency
and
the epicyclic frequency  are written in the form
are written in the form
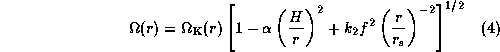
and
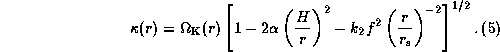
Here, 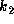 is the apsidal motion constant and
f is a measure of the central star's rotation rate, defined by
is the apsidal motion constant and
f is a measure of the central star's rotation rate, defined by

where 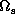 is the angular frequency of the central star
(Papaloizou et al. 1992; Savonije, Heemskerk 1993).
Note that the second and third terms in each square brackets
in equations (4) and (5) denote
the contribution due to the pressure-gradient force in the disk and
the quadrupole contribution to the potential of
the rotationally distorted central star, respectively.
is the angular frequency of the central star
(Papaloizou et al. 1992; Savonije, Heemskerk 1993).
Note that the second and third terms in each square brackets
in equations (4) and (5) denote
the contribution due to the pressure-gradient force in the disk and
the quadrupole contribution to the potential of
the rotationally distorted central star, respectively.
In the remainder of this subsection
we discuss the effect of the rotational deformation
of the central star.
Papaloizou et al. (1992) and Savonije and Heemskerk (1993)
claimed that m=1 oscillations are confined
to the inner part of Be-star disks by
including the quadrupole contribution to the potential
of a rotationally distorted central star.
In Okazaki (1991), since the m=1 oscillations were not confined naturally,
truncation of the disk was assumed.
We show in the following paragraphs that the above conclusions
obtained by Papaloizou et al. (1992) and Savonije and Heemskerk (1993)
do not generally hold for Be-star disks.
For Be stars,
the effect of the rotational deformation of the central star is
comparable even in the innermost region of the disk,
and decreases rapidly with increasing r.
Papaloizou et al. (1992) adopted 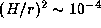 ,
which corresponds to the disk temperature,
,
which corresponds to the disk temperature,
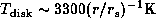 , for a B0-type star and
, for a B0-type star and
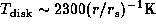 for a B5-type star.
This temperature is too low as a model for the Be-star disks.
Savonije and Heemskerk (1993) studied m=1 oscillations
in disks with
for a B5-type star.
This temperature is too low as a model for the Be-star disks.
Savonije and Heemskerk (1993) studied m=1 oscillations
in disks with 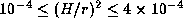 and
and
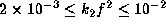 around a star of
around a star of 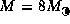 and
and 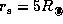 .
These parameter ranges cover
.
These parameter ranges cover
 and
and
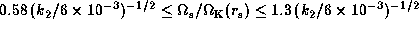 .
Here, we normalized
.
Here, we normalized 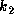 using the value adopted in
Papaloizou et al. (1992).
The value of
using the value adopted in
Papaloizou et al. (1992).
The value of 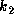 strongly depends on the internal structure
of the star,
and is not determined well (Claret, Giménez 1991).
If
strongly depends on the internal structure
of the star,
and is not determined well (Claret, Giménez 1991).
If 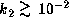 , the above range of the stellar rotation rate
covers that for actual Be stars.
However, the temperature range in their study was still too low
to apply to the Be-star disks.
, the above range of the stellar rotation rate
covers that for actual Be stars.
However, the temperature range in their study was still too low
to apply to the Be-star disks.
We can evaluate the effects by the pressure force and
the rotational deformation of the central star
for the present disk model
by studying the free-particle precession frequency,
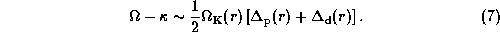
Here, 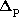 and
and 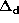 , the measures of
these effects, are given by
, the measures of
these effects, are given by
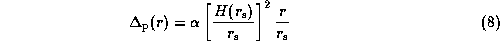
and

For the present model,
the ratio of these two quantities is
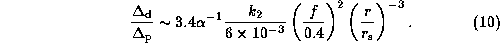
For B0-type Be stars, 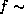 0.2--0.6
(see figure 4 of Kogure, Hirata 1982).
Consequently, the effect of the rotational deformation
of the central star is comparable to
the pressure effect, even in the innermost region of the disk.
For
0.2--0.6
(see figure 4 of Kogure, Hirata 1982).
Consequently, the effect of the rotational deformation
of the central star is comparable to
the pressure effect, even in the innermost region of the disk.
For  , the former is much weaker than the latter.
Thus, we conclude that since the effect of the rotational deformation
of the central star is not generally important in the disks of Be stars,
including this effect does not qualitatively change
the results obtained by Okazaki (1991).
It is important only for the cases
, the former is much weaker than the latter.
Thus, we conclude that since the effect of the rotational deformation
of the central star is not generally important in the disks of Be stars,
including this effect does not qualitatively change
the results obtained by Okazaki (1991).
It is important only for the cases 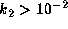 and
and 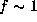 .
.



Next: 2.2 m=1 Perturbation Patterns
Up: 2 m=1 Perturbation Patterns
Previous: 2 m=1 Perturbation Patterns
Atsuo Okazaki
平成9年1月6日 (月), 午後 6時16分22秒
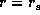 ) to
the outer radius (
) to
the outer radius (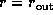 ).
The adopted value of the mean molecular weight was 0.6.
We took a B0 main-sequence star as being a typical central star,
because many Be stars exhibiting long-term V/R variations are
early B stars (Hirata, Hubert-Delplace 1981).
The quantities characterizing the central star were from Allen (1973)
(see table 1 of Paper I).
).
The adopted value of the mean molecular weight was 0.6.
We took a B0 main-sequence star as being a typical central star,
because many Be stars exhibiting long-term V/R variations are
early B stars (Hirata, Hubert-Delplace 1981).
The quantities characterizing the central star were from Allen (1973)
(see table 1 of Paper I).
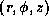 to describe the disk;
the origin is at the center of the star and
the z-axis is perpendicular to the disk midplane.
For convenience's sake, we assume in later sections that
the projection of the observer's direction onto the equatorial plane
is at
to describe the disk;
the origin is at the center of the star and
the z-axis is perpendicular to the disk midplane.
For convenience's sake, we assume in later sections that
the projection of the observer's direction onto the equatorial plane
is at 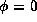 .
.
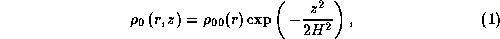
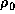 is the unperturbed density,
is the unperturbed density,
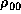 is the unperturbed density on the equatorial plane,
and H is the vertical scale-height of the disk, given by
is the unperturbed density on the equatorial plane,
and H is the vertical scale-height of the disk, given by
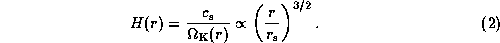
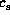 and
and 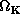 are
the isothermal sound speed and the Keplerian angular frequency,
respectively.
are
the isothermal sound speed and the Keplerian angular frequency,
respectively.
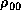 ,
,
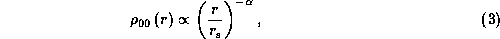
 is a constant.
The surface density is then proportional to
is a constant.
The surface density is then proportional to 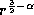 .
.
 and
the epicyclic frequency
and
the epicyclic frequency  are written in the form
are written in the form
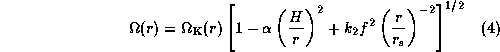
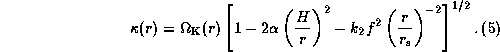
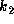 is the apsidal motion constant and
f is a measure of the central star's rotation rate, defined by
is the apsidal motion constant and
f is a measure of the central star's rotation rate, defined by

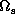 is the angular frequency of the central star
(Papaloizou et al. 1992; Savonije, Heemskerk 1993).
Note that the second and third terms in each square brackets
in equations (
is the angular frequency of the central star
(Papaloizou et al. 1992; Savonije, Heemskerk 1993).
Note that the second and third terms in each square brackets
in equations ( ,
which corresponds to the disk temperature,
,
which corresponds to the disk temperature,
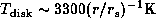 , for a B0-type star and
, for a B0-type star and
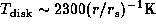 for a B5-type star.
This temperature is too low as a model for the Be-star disks.
Savonije and Heemskerk (1993) studied m=1 oscillations
in disks with
for a B5-type star.
This temperature is too low as a model for the Be-star disks.
Savonije and Heemskerk (1993) studied m=1 oscillations
in disks with 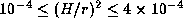 and
and
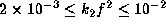 around a star of
around a star of 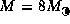 and
and 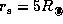 .
These parameter ranges cover
.
These parameter ranges cover
 and
and
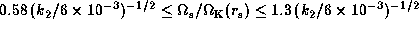 .
Here, we normalized
.
Here, we normalized 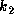 using the value adopted in
Papaloizou et al. (1992).
The value of
using the value adopted in
Papaloizou et al. (1992).
The value of 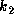 strongly depends on the internal structure
of the star,
and is not determined well (Claret, Giménez 1991).
If
strongly depends on the internal structure
of the star,
and is not determined well (Claret, Giménez 1991).
If 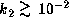 , the above range of the stellar rotation rate
covers that for actual Be stars.
However, the temperature range in their study was still too low
to apply to the Be-star disks.
, the above range of the stellar rotation rate
covers that for actual Be stars.
However, the temperature range in their study was still too low
to apply to the Be-star disks.
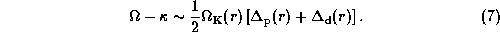
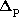 and
and 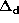 , the measures of
these effects, are given by
, the measures of
these effects, are given by
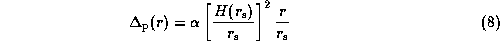

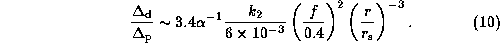
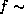 0.2--0.6
(see figure 4 of Kogure, Hirata 1982).
Consequently, the effect of the rotational deformation
of the central star is comparable to
the pressure effect, even in the innermost region of the disk.
For
0.2--0.6
(see figure 4 of Kogure, Hirata 1982).
Consequently, the effect of the rotational deformation
of the central star is comparable to
the pressure effect, even in the innermost region of the disk.
For  , the former is much weaker than the latter.
Thus, we conclude that since the effect of the rotational deformation
of the central star is not generally important in the disks of Be stars,
including this effect does not qualitatively change
the results obtained by Okazaki (1991).
It is important only for the cases
, the former is much weaker than the latter.
Thus, we conclude that since the effect of the rotational deformation
of the central star is not generally important in the disks of Be stars,
including this effect does not qualitatively change
the results obtained by Okazaki (1991).
It is important only for the cases 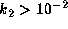 and
and 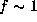 .
.