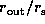 and density-gradient indices
and density-gradient indices  .
.
In Paper I we proposed a model for
the long-term V/R variations of Be stars.
Examining the linear, one-armed, isothermal oscillations in isothermal
equatorial disks, we found that this model well reproduces
the periodicity
of the observed long-term V/R variations for a range of
disk sizes 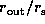 and density-gradient indices
and density-gradient indices  .
.
In this paper we have considered the profile variabilities
of Balmer lines caused by the one-armed isothermal oscillations
studied in Paper I.
In order to examine the effects of one-armed oscillations
on line profiles,
we assumed nonlinear perturbation patterns
similar to the linear m=1 eigenfunctions.
The eigenfunctions were normalized so that
the maximum value of the perturbed part of the angular velocity 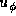 is 10% of the unperturbed part
is 10% of the unperturbed part 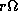 .
In addition, we assumed that the source function is constant
over the entire disk region.
Based on these assumptions, we studied the profile variations
by computing fluxes along a bundle of line-of-sights
for various values of
disk sizes
.
In addition, we assumed that the source function is constant
over the entire disk region.
Based on these assumptions, we studied the profile variations
by computing fluxes along a bundle of line-of-sights
for various values of
disk sizes 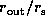 , density gradient indices
, density gradient indices  ,
characteristic optical depths
,
characteristic optical depths 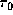 ,
and inclination angles i.
We took only the thermal broadening into account as the line-broadening
mechanism.
As a result of this study, the following conclusions have been derived:
,
and inclination angles i.
We took only the thermal broadening into account as the line-broadening
mechanism.
As a result of this study, the following conclusions have been derived:
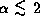 ,
the peak separation is given by
,
the peak separation is given by 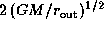 ,
and is independent of the line optical depth.
This is because the largest contribution to the total emission
for
,
and is independent of the line optical depth.
This is because the largest contribution to the total emission
for 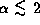 arises from the constant line-of-sight
velocity region
tangent to the disk outer radius.
On the other hand, for a steeper (
arises from the constant line-of-sight
velocity region
tangent to the disk outer radius.
On the other hand, for a steeper (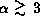 )
density distribution,
the largest contribution arises from the constant line-of-sight
velocity region
tangent to the radius where the optical depths
along the line-of-sights are about unity.
Thus, for
)
density distribution,
the largest contribution arises from the constant line-of-sight
velocity region
tangent to the radius where the optical depths
along the line-of-sights are about unity.
Thus, for 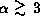 , the peak separation decreases
towards
, the peak separation decreases
towards 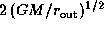 along with an increase in the line optical depth.
along with an increase in the line optical depth.
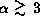 )
density gradients
than for disks with flat (
)
density gradients
than for disks with flat (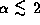 ) density gradients.
This is because the amplitude of the perturbation is
larger for
) density gradients.
This is because the amplitude of the perturbation is
larger for 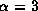 than for
than for 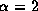 at the region
from which the largest contribution to the total emission
arises.
In principle, this disk-structure dependent feature
can be used to probe the structure of Be-star disks.
at the region
from which the largest contribution to the total emission
arises.
In principle, this disk-structure dependent feature
can be used to probe the structure of Be-star disks.
In this paper we assumed perturbation patterns similar to the linear eigenfunctions and the constant-source function to study the effects of the one-armed oscillations on line profiles. Consideration of the effect of the non-uniform source function is expected to provide only minor modifications to the above conclusions. Taking the nonlinear effects exactly into account, however, can modify the results obtained in this paper, since the amplitude of the V/R variation depends on the detailed forms of the eigenfunctions. In addition, the periods and eigenfunctions are sensitive to the disk models adopted. Therefore, it is highly desired to investigate the nonlinear one-armed modes in equatorial disks of Be stars.
It is a pleasure to thank R. Hirata, S. Kato, M. Mon, and T. Horaguchi for stimulating discussions. The hospitalities of the Department of Astronomy, Kyoto University and Astronomical Institute, University of Amsterdam are also greatly appreciated. The author wishes to acknowledge financial support of the Foundation for Inservice Trading and Welfare of the Private School Personnel. This work was partially supported by a grant from the Hokkai-Gakuen Educational Foundation.