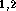
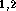
 Institute of Astronomy 'Anton Pannekoek',
University of Amsterdam,
Kruislaan 403,
1098 SJ Amsterdam, The Netherlands.
Institute of Astronomy 'Anton Pannekoek',
University of Amsterdam,
Kruislaan 403,
1098 SJ Amsterdam, The Netherlands.
 College of General Education,
Hokkai-Gakuen University,
Toyohira-ku, Sapporo 062, Japan.
College of General Education,
Hokkai-Gakuen University,
Toyohira-ku, Sapporo 062, Japan.
e-mail: okazaki@elsa.hokkai-s-u.ac.jp
Abstract.
We discuss the characteristics of the outflow in discs of Be stars,
based on the viscous decretion disc scenario.
Solving the wind equation,
we find that a transonic solution exists for any  .
The sonic point is located at r > 100 R
for plausible values of parameters,
where R is the stellar radius.
The sonic radius is smaller for higher temperature
and/or larger radiative force.
We also find that
the topology of the sonic point is nodal for
.
The sonic point is located at r > 100 R
for plausible values of parameters,
where R is the stellar radius.
The sonic radius is smaller for higher temperature
and/or larger radiative force.
We also find that
the topology of the sonic point is nodal for 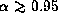 ,
while it is saddle type for
,
while it is saddle type for 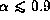 .
In the subsonic region, the outflow velocity
increases as r and
the surface density decreases as
.
In the subsonic region, the outflow velocity
increases as r and
the surface density decreases as 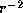 .
The angular velocity of the disc decreases as
.
The angular velocity of the disc decreases as 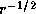 in the inner subsonic region,
while it decreases as
in the inner subsonic region,
while it decreases as 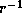 in the outer subsonic region.
in the outer subsonic region.
keywords: hydrodynamics -- stars: circumstellar matter -- stars: emission line, Be -- stars: mass loss
Be stars are non-supergiant early-type stars
with Balmer emission lines,
whose spectral types range from late O- to early A-type.
Extensive studies have revealed that a Be star has
a two-component extended atmosphere,
a polar region and a cool disc-like region.
The polar region consists of a low-density, fast outflow
emitting UV radiation.
The mass loss rate of this region inferred from the UV lines
is about 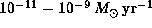 (Snow 1981).
(Snow 1981).
In contrast to the polar region, the disc region consists of a high-density plasma whose outflow velocity is small. The optical emission lines and the IR excess arise from this region. Unfortunately, the nature of this region is not well understood, depsite that large observational efforts have been devoted to the study of Be stars.
Lee et al. (1991) constructed a disc model, in which matter rotates at Keplerian speed but gradualy drifts outward because of the effect of viscosity. Assuming Keplerian rotation and neglecting the advective term in the equation of momentum coservation, they obtained steady structure of viscous decretion discs around Be stars. The purpose of this paper is to study the characteristics of the outflow in viscous decretion discs around Be stars.
We assume that the circumstellar disc of a Be star is steady, geometrically thin, and symmetric about the rotational axis and the equatorial plane. Moreover, we assume for simplicity that the disc is isothermal, and adopt the Shakura-Sunyaev viscosity prescription. Since the deviation from a point mass potential due to the rotational distortion of the star is small in general, we neglect the quadrupole contribution to the gravitational potential. We assume that the radiative acceleration arises from the absorption of stellar continuum by an ensemble of optically-thin weak lines, and adopt the parametric form for the radiative force proposed by Chen & Marlborough (1994).
From the vertically integrated equations describing the mass, momentum, and angular momentum conservation in a disc around a star of mass M and radius R, together with the equation of state and the Shakura-Sunyaev viscosity prescription, we obtain the following equations which describe the stationary viscous flow.
where 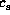 is the isothermal sound speed,
is the isothermal sound speed,
 is a viscosity parameter,
is a viscosity parameter,
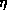 and
and  are parameters which characterize
the radiative force, and
are parameters which characterize
the radiative force, and
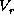 and
and 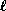 are
the vertically-averaged radial velocity and
specific angular momentum, respectively.
The subscript 's' denotes the quantities
at the sonic point.
are
the vertically-averaged radial velocity and
specific angular momentum, respectively.
The subscript 's' denotes the quantities
at the sonic point.
It is important to note that, in the current problem,
the angular momentum distribution of the flow is not
given a priori but obtained as the solution of
Eqs. (1) and (2);
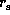 and
and 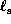 are the eigenvalues of
these equations.
Note also that Eq. (2) indicates that
a tiny deviation from the Keplerian rotation can cause
a drastic change in the radial velocity distribution.
are the eigenvalues of
these equations.
Note also that Eq. (2) indicates that
a tiny deviation from the Keplerian rotation can cause
a drastic change in the radial velocity distribution.
In the following examples,
the central star is a B0 main-sequence star with 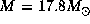 ,
,
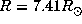 , and
, and 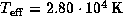 (Allen 1973).
Since, the disc is assumed to be isothermal,
the structure of the viscous transonic outflow is independent of
the mass decretion rate
[see Sec. 3 of Abramowicz & Kato (1989)].
(Allen 1973).
Since, the disc is assumed to be isothermal,
the structure of the viscous transonic outflow is independent of
the mass decretion rate
[see Sec. 3 of Abramowicz & Kato (1989)].
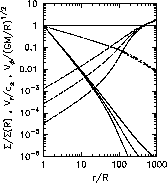
Figure 1: Structure of
the viscous transonic decretion disc
for 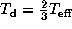 and
and 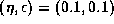 ,
where
,
where 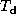 is the disc temperature.
Solid, dashd, and dash-dotted lines denote
is the disc temperature.
Solid, dashd, and dash-dotted lines denote
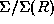 ,
, 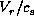 , and
, and 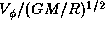 ,
respectively.
Thick lines, lines with intermediate thickness, and thin lines
are for
,
respectively.
Thick lines, lines with intermediate thickness, and thin lines
are for 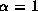 ,
, 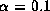 , and
, and 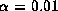 ,
respectively
,
respectively
Figure 1 shows a typical structure of
the viscous transonic decretion disc.
From Fig. 1, we find that the sonic point is located
far from the star and the outflow is highly subsonic
for 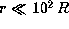 .
This is because it is basically the pressure force
which accelerates the flow up to a supersonic speed.
Consequently, the sonic radius is smaller for higher disc temperature
and/or larger radiative force.
.
This is because it is basically the pressure force
which accelerates the flow up to a supersonic speed.
Consequently, the sonic radius is smaller for higher disc temperature
and/or larger radiative force.
We also find that, in the subsonic part of the disc,
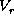 increases as r and
increases as r and
 decreases as
decreases as 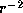 .
In the inner subsonic region,
.
In the inner subsonic region,
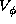 decreases as
decreases as 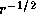 ,
while in the outer subsonic region it decreases as
,
while in the outer subsonic region it decreases as 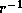 .
It should be noted that these radial dependences
hold in general in viscous decretion discs.
.
It should be noted that these radial dependences
hold in general in viscous decretion discs.
Our results, together with the observed range of the base density for Be star discs (Dougherty et al. 1994), suggest that the mass loss rate in the equatorial region is at most comparable with that in the polar region.
It is well known that the stability of the transonic accretion
with Shakura-Sunyaev viscosity prescriptions
is related to the topology of the sonic point
(e.g., Abramowicz & Kato 1989, and references therein).
For  greater than a critical value,
the sonic point is nodal and
the transonic accretion is unstable.
On the other hand, for
greater than a critical value,
the sonic point is nodal and
the transonic accretion is unstable.
On the other hand, for  smaller than the critical value,
the sonic point is saddle type and the stable transonic accretion
exists.
The instability arises as a result of work done by viscous force
[see Kato et al. (1988) for detailed analysis].
smaller than the critical value,
the sonic point is saddle type and the stable transonic accretion
exists.
The instability arises as a result of work done by viscous force
[see Kato et al. (1988) for detailed analysis].
Figure 2: Diagram showing the location of the sonic points
in the 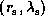 -plane
for (a)
-plane
for (a) 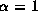 and (b)
and (b) 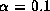 , where
, where
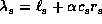 is normalized by
is normalized by 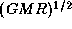 .
Each curve denotes the relation between
.
Each curve denotes the relation between 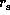 and
and
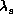 for a constant sound speed.
From the bottommost curve upwards
for a constant sound speed.
From the bottommost curve upwards
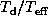 = 1.0, 0.82, 0.64, 0.46, 0.28,
and 0.10.
The filled circle on each curve indicates the position
of the sonic point.
The dashed line separates the spiral-type sonic point region
(upper side of the line)
from the nodal-type sonic point region (lower side of the line),
and the dash-dotted line separates
the nodal-type region (upper side)
from the saddle-type region (lower side).
In Fig. 2(b) the nodal-type region is
so narrow that it is indistinguishable on the figure.
The thin line in Fig. 2(a) indicates
the bounrary in the parameter space
below which the circular orbit at the sonic radius is unstable
= 1.0, 0.82, 0.64, 0.46, 0.28,
and 0.10.
The filled circle on each curve indicates the position
of the sonic point.
The dashed line separates the spiral-type sonic point region
(upper side of the line)
from the nodal-type sonic point region (lower side of the line),
and the dash-dotted line separates
the nodal-type region (upper side)
from the saddle-type region (lower side).
In Fig. 2(b) the nodal-type region is
so narrow that it is indistinguishable on the figure.
The thin line in Fig. 2(a) indicates
the bounrary in the parameter space
below which the circular orbit at the sonic radius is unstable
In Fig. 2, we present an example
showing the location of the sonic points
in the 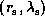 -plane.
As shown in Fig. 2, in our model,
the topology of the sonic point is nodal for
-plane.
As shown in Fig. 2, in our model,
the topology of the sonic point is nodal for 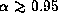 ,
while it is saddle type for
,
while it is saddle type for 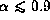 .
This means that
the stationary transonic decretion in discs of Be stars
exists if
.
This means that
the stationary transonic decretion in discs of Be stars
exists if 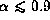 , whereas
the transonic decretion cannot be stationary
if
, whereas
the transonic decretion cannot be stationary
if 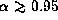 .
.
Abramowicz, M.A., Kato, S., 1989, ApJ 336, 304
Allen, C.W., 1973, Astrophysical Quantities, 3rd ed. The Athlone Press, London, pp.206, 209
Chen, H., Marlborough, J.M., 1994, ApJ 427, 1005
Dougherty, S.M., Waters, L.B.F.M., Burki, G., et al., A&A 290, 609
Kato, S., Honma, F., Matsumoto, R., 1988, MNRAS 231, 37
Lee, U., Saio, H., Osaki, Y., 1991, MNRAS 250, 432
Snow, T.P., 1981, ApJ 251, 139