Astronomical Institute 'Anton Pannekoek',
University of Amsterdam,
Kruislaan 403,
1098 SJ Amsterdam, The Netherlands
College of General Education, Hokkai-Gakuen University,
Toyohira-ku, Sapporo 062, Japan
(okazaki@elsa.hokkai-s-u.ac.jp)
In SU Ursa Majoris (SU UMa) stars, which constitute a subclass of dwarf novae, the accretion disks are considered to be eccentric during superoutbursts (e.g., Osaki 1996, and references therein). It is natural to regard this eccentricity as the manifestation of global m=1 modes. Using a vertically-integrated disk model, Hirose & Osaki (1993) analysed the m=1 modes confined to the outermost part of the disk and found the eigenfrequencies consistent with the observed periods of superhumps. In this paper, we examine the two-dimensional structure of the m=1 eigenmodes in disks of SU UMa stars.
We take a geometrically thin,
axisymmetric, polytropic disk around a white dwarf
as an unperturbed disk.
We assume that the unperturbed disk, which is in hydrostatic equilibrium
in the vertical direction,
is truncated at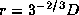 
by the tidal instability,
where D is the binary separation.
We use the phase-averaged axisymmetric potential
for the tidal potential.
We neglect the radial advective motion and viscous effects.
We consider a linear, m=1 adiabatic perturbation.
We solve the resulting second-order
partial differential equation for the enthalpy perturbation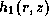 
only in the propagation region, which extends
from the inner Lindblad resonance (ILR) to the disk outer radius.
As the boundary conditions,
we require that the Lagrangian perturbation of the pressure
vanishes on the disk surface and the disk outer radius,
and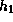 
is regular at the ILR.
Figure 1 presents the even (eccentric) and the odd (warping) fundamental modes confined to the outermost part of the disk with parameters typical for SU UMa stars. These modes prograde and have periods of several percent of the binary period. Therefore, both modes naturally explain the superhump periods which are always longer by a few percent than the orbital period.
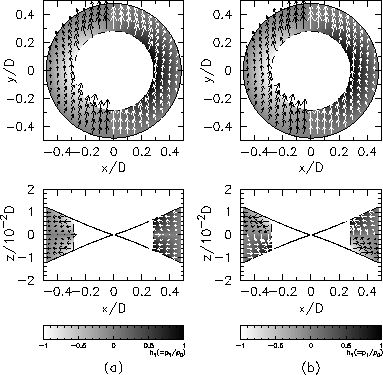
Figure 1: The fundamental mode confined to the outermost part
of the disk:
(a) the even mode and (b) the odd mode.
The upper panel shows the 
-distribution
of the perturbations averaged vertically over
the upper half-thickness,
while the lower panel shows
the 
-distribution of the perturbations.
A gray-scale representation denotes
the distribution of 
.
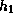Arrows denote the perturbed velocity vectors
The eigenfunctions of the eccentric mode and the warping mode are quite similar, except for the parity of the mode and the perturbed velocity field near the equatorial plane. The difference in the disk geometry caused by these two kinds of modes may be detectable.