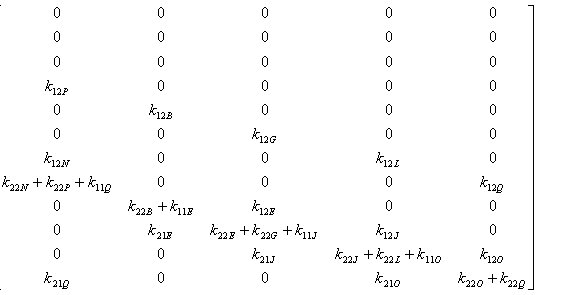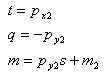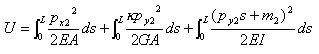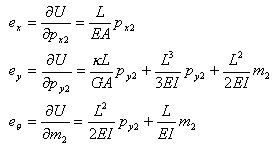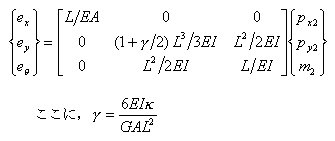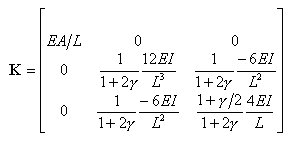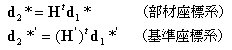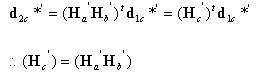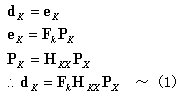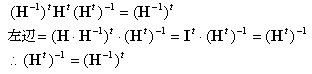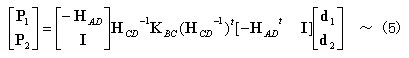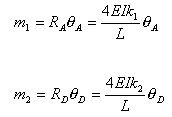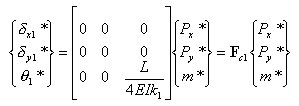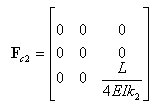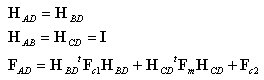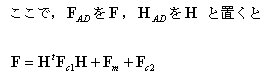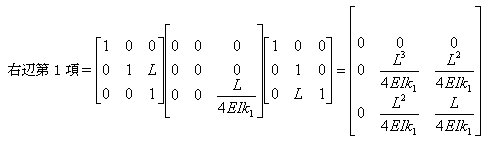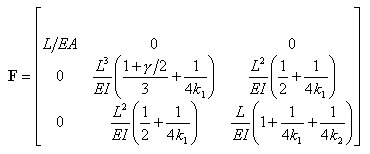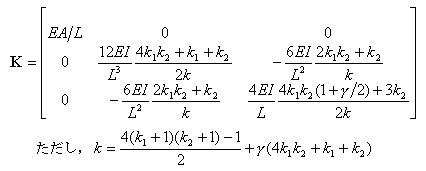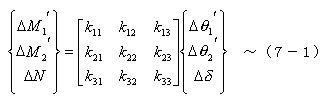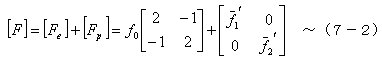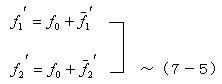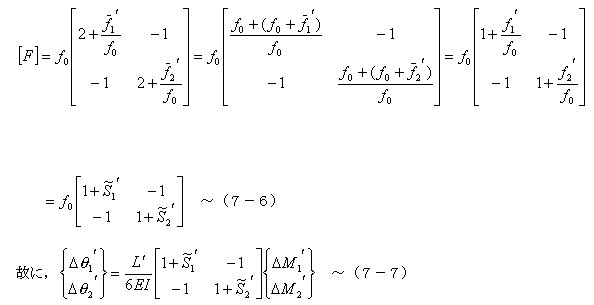丂丂丂丂崪慻峔憿夝愅乮儅僩儕僢僋僗峔憿夝愅乯
丂丂丂丂丂丂丂丂栚師
 崪慻峔憿夝愅偺婎慴
崪慻峔憿夝愅偺婎慴
 丂懡尦楢棫侾師曽掱幃偺夝朄
丂懡尦楢棫侾師曽掱幃偺夝朄
 丂梫慺崉惈儅僩儕僢僋僗
丂梫慺崉惈儅僩儕僢僋僗
 丂掁崌忦審丆揔崌忦審
丂掁崌忦審丆揔崌忦審
 丂慡懱崉惈儅僩儕僢僋僗偺嶌惉
丂慡懱崉惈儅僩儕僢僋僗偺嶌惉
 丂偣傫抐曄宍丆崉堟偍傛傃嵽抂夞揮偽偹偺庢傝埖偄
丂偣傫抐曄宍丆崉堟偍傛傃嵽抂夞揮偽偹偺庢傝埖偄
 丂晹嵽儌僨儖
丂晹嵽儌僨儖
 丂棜楌懃偲暅尦椡摿惈
丂棜楌懃偲暅尦椡摿惈
 丂夝愅僾儘僌儔儉
丂夝愅僾儘僌儔儉
丂寶抸峔憿夝愅摿榑嘦偺僩僢僾儁乕僕傊栠傞
乮1乯丂崪慻峔憿夝愅偺婎慴
丂島媊偱埖偆斖埻丂丗曄埵朄偵傛傞暯柺崪慻偺惷揑慄宍夝愅偍傛傃惷揑旕慄宍夝愅偵尷掕
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂惷揑旕慄宍夝愅丂乣丂旕慄宍嫇摦偺梫場
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丒嵽椏旕慄宍乮梫慺儗儀儖丆晹嵽儗儀儖乯
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丒婔壗妛揑旕慄宍乮椺偊偽丆俹亅儮岠壥乯
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂島媊偱偼晹嵽儗儀儖偺嵽椏旕慄宍偺傒傪峫椂
丂椡妛偺億僀儞僩乣丂嘆丂僗儉乕僗側椡偺棳傟偵懳偡傞攝椂乮屆揟揑側峔憿椡妛傪梡偄偨
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂庤寁嶼偍傛傃僷儔儊僩儕僢僋丒僗僞僨傿乕偱捈姶椡傪梴惉乯
丂丂丂丂丂丂丂丂丂丂丂丂丂 嘇丂愡揰偵偍偗傞椡偺掁崌幃惉棫偺妋擣乮寁嶼寢壥偺僠僃僢僋偺婎杮乯
丂丂丂丂丂丂丂丂丂丂丂丂丂椺偊丆僾儘僌儔儉偵儈僗偑堦愗側偔偲傕丆巊偄庤偑岆傟偽摼傜傟偨寢壥偵
丂丂丂丂丂丂丂丂丂丂丂丂岆傝偑惗偠傞嫲傟偑偁傞丆岆傝偑側偔偲傕椡妛揑側僶儔儞僗偵寚偗傞嫲傟傕
丂丂丂丂丂丂丂丂丂丂丂丂偁傞丅廬偭偰丆忋婰偺億僀儞僩傪娞偵柫偠偰丆忢偵嵶怱偺拲堄傪暐偆偙偲偑
丂丂丂丂丂丂丂丂丂丂丂丂戝愗偱偁傞丅
丂儅僩儕僢僋僗峔憿夝愅偺摿挜丂丗丂峔憿椡妛偺婎慴揑奣擮傪拪徾壔丆堦斒壔偟偰偄傞偨傔丆
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂夝愅朄偺峫偊曽偵偼僩儔僗傗儔乕儊儞偺嬫暿丆2師尦丆3師
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂尦偺嬫暿偑柍偄丅堘偄偼1愡揰摉偨傝偺帺桼搙悢偑堎側
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂傞偩偗偱偁傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂曄埵朄偵傛傞掁崌曽掱幃嶌惉偺僼儘乕
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂俹亖俲倓丂乮愡揰壸廳乣愡揰曄埵娭學幃乯
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂1乯丂晹嵽偺峔惉曽掱幃乮constitutive equations
)
丂丂丂丂丂
| 丂晹嵽抂壸廳乣晹嵽抂曄埵丂娭學乮晹嵽嵗昗宯乯丂乣乮1乯 |
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂伀 嵗昗曄姺乮婎弨嵗昗宯仼晹嵽嵗昗宯乯
| 晹嵽抂壸廳乣晹嵽抂曄埵丂娭學乮婎弨嵗昗宯乯丂乣乮2乯 |
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂2乯丂揔崌忦審幃( compatibility equations )
| 晹嵽抂曄埵乣愡揰曄埵丂娭學乮婎弨嵗昗宯乯丂乣乮3乯 |
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂伀丂乮3乯傪乮2乯偵戙擖
| 晹嵽抂壸廳乣愡揰曄埵丂娭學乮婎弨嵗昗宯乯丂乣乮4乯 |
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂3乯丂掁崌忦審幃( equilibrium equations )
| 愡揰壸廳乣晹嵽抂壸廳丂娭學乮婎弨嵗昗宯乯丂乣乮5乯 |
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂伀丂乮5乯偵乮4乯傪戙擖
愡揰壸廳乣愡揰曄埵丂娭學乮婎弨嵗昗宯乯丂乣乮6乯
俹亖俲倓 |
丂愡揰丆晹嵽丆壸廳偍傛傃曄埵偺婰崋乮崪慻峔憿夝愅僥僉僗僩偺椺乯
丂丂丂丂丂丂愡揰柤丂丂丂丂丂丂丗丂塸戝暥帤丂俙丆俛丆俠丆.....偱昞偡丅側偍巟揰偼俷偱昞偡丅
丂丂丂丂丂丂晹嵽柤丂丂丂丂丂丂丗丂塸彫暥帤丂a,b,c,d,...偱昞偡丅
丂丂丂丂丂丂晹嵽抂偺嬫暿丂丗丂1抂乮僗僞乕僩揰乯丆2抂乮僄儞僪揰乯丅愡揰偺塸暥帤偺傾儖僼傽儀僢僩
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂弴偑憗偄曽偐傜抶偄曽偵岦偐偆偲栺懇丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂側偍丆巟揰俷偼懠偺塸暥帤傛傝愭偵偁傞偲偡傞丅
丂丂丂丂丂丂壸廳儀僋僩儖丂丂丗丂倫亖乷倫倶丂倫倷丂倣乸乫丂偙偙偱丆乫偼揮抲偺堄枴丅埲壓摨條丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂偨偩偟丆倫倶乣嵽幉曽岦壸廳丆倫倷乣嵽幉捈岎曽岦壸廳丆
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂倣乣儌乕儊儞僩
丂丂丂丂丂丂愡揰壸廳丂丂丂丂丗丂愡揰偺塸暥帤傪揧偊倫俙丆倫俛丆...偺傛偆偵昞偡丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂倫俙亖乷倫倶俙丂倫倷俙丂倣俙乸乫
丂丂丂丂丂丂晹嵽抂壸廳丂丂丂丗丂晹嵽柤偲偳偪傜偺抂晹偐傪帵偝偹偽側傜側偄偺偱丆揧偊帤偼2偮丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂倫1a丆倫2a丆p1b丆p2b丆....
丂丂丂丂丂丂曄埵儀僋僩儖 丂丂丗丂倓亖乷兟倶丂兟倷丂儲乸乫丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂偨偩偟丆兟倶乣嵽幉曽岦曄埵乮扨埵丗挿偝乯丆兟倷乣嵽幉捈岎曽岦
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂曄埵丆儲乣夞揮妏乮扨埵丗儔僕傾儞乯
丂丂丂丂丂丂愡揰曄埵丂丂丂丂丗丂倓俙丆倓俛丆....偺傛偆偵愡揰柤傪揧偊傞丅
丂丂丂丂丂丂晹嵽抂曄埵丂丂丂丗丂倓1a丆倓2a丆倓1b丆倓2b丆...
丂壸廳丆曄埵偺晞崋偺婯栺
丂丂丂丂丂丂晹嵽抂壸廳丆晹嵽抂曄埵乮晹嵽嵗昗宯乯偍傛傃愡揰壸廳丆愡揰曄埵乮婎弨嵗昗宯乯
丂丂丂丂丂乣塃庤嵗昗宯偵廬偆丅懄偪丆倶幉曽岦偺椡丆曄埵偼悈暯塃岦偒乮晹嵽嵗昗宯偺応崌
丂丂丂丂丂嵽幉曽岦偺椡丆曄埵偼丆1抂偐傜2抂傊岦偐偆曽岦乯傪惓丆倷幉曽岦偺椡丆曄埵偼墧捈
丂丂丂丂丂忋岦偒乮晹嵽嵗昗宯偺応崌丆嵽幉偵捈岎曽岦偺椡丆曄埵偼倶幉偺惓曽岦偲側偡妏偑
丂丂丂丂丂斀帪寁夢傝偵90搙乯傪惓丆儌乕儊儞僩偲夞揮妏偼斀帪寁夢傝傪惓偲偡傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂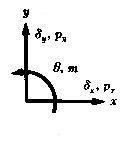
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂恾丂1-1丂壸廳丆曄埵偺晞崋偺婯栺乮惓曽岦乯
丂丂丂丂丂丂億僀儞僩丂乣丂晹嵽抂壸廳丆晹嵽抂曄埵偺晞崋偺婯栺偲晹嵽墳椡偺晞崋偺婯栺傪
丂丂丂丂丂丂丂丂丂丂丂丂丂丂嬫暿偟丆崿摨偟側偄偙偲丅
丂丂丂丂丂晹嵽墳椡偺晞崋偺婯栺丂丗丂姷椺偵傛傟偽丆幉曽岦椡丗堷挘傪惓丆偣傫抐椡丗仾伀傪
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂惓丆儌乕儊儞僩丗忋懁埑弅偱壓懁堷挘偲側傞1懳偺儌乕
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂儊儞僩傪惓偲偡傞丅
丂婎弨嵗昗宯偲晹嵽嵗昗宯
丂丂丂丂丂婎弨嵗昗宯偼慡懱嵗昗宯丆global嵗昗宯丆晹嵽嵗昗宯偼嬊晹嵗昗宯丆local嵗昗宯
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂偲傕屇偽傟傞丅
丂丂丂丂丂丂婎弨嵗昗宯丂丗丂崪慻慡懱偵揔梡偡傞嵗昗宯
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂倶乫幉悈暯塃岦偒傪惓丆倷乫幉墧捈忋岦偒傪惓丆夞揮偼斀帪寁夢傝傪
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂惓偲偡傞丅晹嵽嵗昗宯偲嬫暿偡傞偨傔偵丆偙偙偱偼乫傪晅偗偰偄傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂嵗昗偺尨揰偼丆僨乕僞乮椺偊偽丆愡揰偺嵗昗抣僨乕僞乯偺擖椡偑
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂娙扨偵側傞傛偆偵慖傇丅
丂丂丂丂丂丂晹嵽嵗昗宯丂丗丂屄乆偺晹嵽偵揔梡偡傞嵗昗宯乮椺偊偽丆幬嵽偼幬嵽側傝偵埲壓偺
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂傛偆偵峫偊傞乯
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂倶幉偼1抂偐傜2抂傊岦偐偆曽岦傪惓丆倷幉偼嵽幉偵捈岎偱倶幉偲偺
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂側偡妏偑斀帪寁夢傝偵90搙傪惓丆夞揮偼斀帪寁夢傝傪惓偲偡傞丅
丂丂丂丂丂丂丂丂
丂丂丂丂丂丂丂丂忋婰嵗昗宯傪峫椂偡傞偲丆愡揰壸廳倫俙丆倫俛丆...丆愡揰曄埵倓俙丆倓俛丆...偼忢偵
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮婎弨嵗昗宯乯偱昞偡丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂晹嵽抂壸廳丆晹嵽抂曄埵偼昁梫偵墳偠偰乮婎弨嵗昗宯乯偲
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮晹嵽嵗昗宯乯傪巊偄暘偗傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂晹嵽抂壸廳丂倫1a丆倫2a丆p1b丆p2b丆....丂丂丂丂丂丂丗丂乮晹嵽嵗昗宯乯
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂倫1a乫丆倫2a乫丆p1b乫丆p2b乫丆...丂丂丂丂丗丂乮婎弨嵗昗宯乯
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂晹嵽抂曄埵丂倓1a丆倓2a丆倓1b丆倓2b丆..丂丂丂丂丂丂丗丂乮晹嵽嵗昗宯乯
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂倓1a乫丆倓2a乫丆倓1b乫丆倓2b乫丆..丂丂丂丂丗丂乮婎弨嵗昗宯乯
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂婎弨嵗昗宯偱昞帵偟偨壸廳丆曄埵偵偼丆乫傪晅偗偰晹嵽嵗昗宯偲
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂嬫暿偡傞丅
丂嵗昗曄姺儅僩儕僢僋僗
丂丂丂丂丂晹嵽嵗昗宯偱昞帵偟偨検乮壸廳丆曄埵乯傪婎弨嵗昗宯偱昞帵偟捈偟偨傝丆媡偵婎弨
丂丂丂丂嵗昗宯偱昞帵偟偨検乮壸廳丆曄埵乯傪晹嵽嵗昗宯偱昞帵偟偨検偵捈偡偙偲傪嵗昗曄姺偲
丂丂丂丂塢偆丅屳偄偵堎側傞嵗昗宯偱昞偟偨2偮偺検偼丆嵗昗曄姺儅僩儕僢僋僗傪夘偟偰娭學晅偗
丂丂丂丂傜傟傞丅
丂丂丂丂丂丂晹嵽抂壸廳偺嵗昗曄姺
丂丂丂丂丂丂丂丂丂丂晹嵽嵗昗宯偱昞帵偟偨壸廳傪丂倫倶丆倫倷丆倣
丂丂丂丂丂丂丂丂丂丂婎弨嵗昗宯偱昞帵偟偨壸廳傪丂倫倶乫丆倫倷乫丆倣乫丂偲抲偔丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂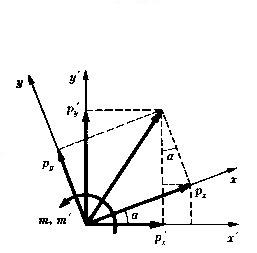
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂恾丂1亅2丂晹嵽抂壸廳偺嵗昗曄姺
丂丂丂丂丂丂丂丂丂丂丂忋恾傪嶲徠偡傞偲丆晹嵽偺嵽幉曽岦倶偑婎弨嵗昗偺倶乫幉偵懳偟偰妏搙兛
丂丂丂丂丂丂丂丂丂丂丂孹偄偰偄傞偲偒丆椉幰偺壸廳娫偺娭學幃偼師偺傛偆偵側傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂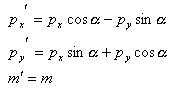
丂丂丂丂丂丂丂丂丂丂丂忋偺幃傪儅僩儕僢僋僗昞帵偡傞偲丆
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂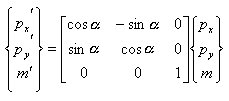
丂丂丂丂丂丂丂丂丂丂丂娙寜偵婰弎偡傞偲丆
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂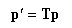
丂丂丂丂丂丂晹嵽抂曄埵偺嵗昗曄姺
丂丂丂丂丂丂丂丂丂丂晹嵽嵗昗宯偱昞帵偟偨曄埵傪丂兟倶丆兟倷丆儲
丂丂丂丂丂丂丂丂丂丂婎弨嵗昗宯偱昞帵偟偨曄埵傪丂兟倶乫丆兟倷乫丆儲乫偲抲偔丅
丂丂丂丂丂丂丂丂丂丂丂丂丂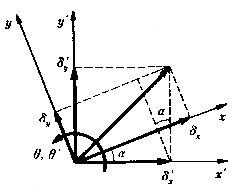
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂恾丂1-3丂晹嵽抂曄埵偺嵗昗曄姺
丂丂丂丂丂丂丂丂丂丂丂忋恾傪嶲徠偡傞偲丆椉幰偺曄埵娫偺娭學幃偼師偺傛偆偵側傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂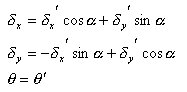
丂丂丂丂丂丂丂丂丂丂丂忋偺幃傪儅僩儕僢僋僗昞帵偡傞偲丆
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂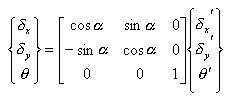
丂丂丂丂丂丂丂丂丂丂丂娙寜偵婰弎偡傞偲丆
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂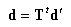
丂梫慺崉惈儅僩儕僢僋僗
丂丂丂丂丂偙傟偵偮偄偰偼丆乮3乯梫慺崉惈儅僩儕僢僋僗偺崁偵偍偄偰丆晹嵽抂壸廳乣晹嵽抂曄埵
丂丂丂丂娭學乮晹嵽嵗昗宯昞帵乯偺崉惈儅僩儕僢僋僗偺桿摫偲晹嵽抂壸廳乣晹嵽抂曄埵娭學
丂丂丂丂乮婎弨嵗昗宯昞帵乯傊偺曄姺偵偮偄偰愢柧偟偰偄傞偺偱丆偦偪傜傪嶲徠偺偙偲丅
丂丂丂丂丂側偍丆愡揰壸廳乣愡揰曄埵娭學偺崉惈儅僩儕僢僋僗偺抲偒姺偊偵偮偄偰偼丆乮4乯掁崌
丂丂丂丂忦審丆揔崌忦審偺崁傪嶲徠偺偙偲丅
丂
丂摍壙愡揰壸廳
丂丂丂丂丂扨撈偺晹嵽偺椉抂偺愡揰偵嫴傑傟偨晹嵽幉偵嶌梡偡傞壸廳乮椺偊偽丆摍暘晍壸廳傗
丂丂丂丂廤拞壸廳側偳乯偺偙偲傪拞娫壸廳偲偄偆丅儅僩儕僢僋僗峔憿夝愅偱偼丆慄宍抏惈嫇摦傪
丂丂丂丂壖掕偡傞応崌丆廳偹崌傢偣偺尨棟偑惉棫偡傞偺偱丆拞娫壸廳傪偙傟偲摍壙側愡揰壸廳
丂丂丂丂偵抲偒姺偊偰寁嶼傪幚峴偡傞丅
丂丂丂丂丂嬶懱揑側摍壙愡揰壸廳偺峫偊曽丆庢傝埖偄偼壓恾傪嶲徠偡傞偲丆埲壓偺捠傝偱偁傞丅
丂丂丂丂丂丂丂丂丂丂丂丂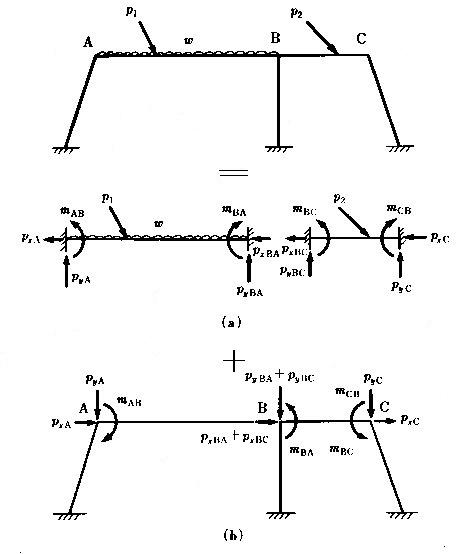
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂恾丂1-4丂壸廳宯乮倎乯偲壸廳宯乮倐乯偺廳偹崌傢偣
丂丂丂丂丂丂丂壸廳宯乮倎乯丒丒丒丒拞娫壸廳偑嶌梡偟偰偄傞晹嵽傪扨撈偵庢傝弌偟丆椉抂屌掕晹嵽偲
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂傒側偟偨偲偒偺屌掕抂斀椡丆屌掕抂儌乕儊儞僩傪媮傔傞丅偙傟傪
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂壸廳宯乮倎乯偲偡傞丅
丂丂丂丂丂丂丂壸廳宯乮倐乯丒丒丒丒幚嵺偺峔憿暔偵偼丆壸廳宯(a)偱壖掕偟偨愡揰曄埵偲夞揮傪峉懇偡傞
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂椡傗儌乕儊儞僩偼嶌梡偟偰偄側偄偺偱丆忋偱媮傔偨屌掕抂斀椡丆屌掕
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂抂儌乕儊儞僩偺晞崋傪媡偵偟偰摍壙愡揰壸廳偲偟丆崪慻偵嶌梡偝偣傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂偙偺宯偵偮偄偰捠忢偺儅僩儕僢僋僗峔憿夝愅傪峴偆丅
丂丂丂丂拞娫壸廳偑嶌梡偟偰偄傞晹嵽偺墳椡嶼掕亖
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂壸廳宯乮倐乯偺晹嵽墳椡亄壸廳宯乮倎乯偺晹嵽墳椡
丂丂丂丂丂偙偺壛嶼偵傛傝丆壸廳宯乮倎乯偺屌掕抂斀椡丆屌掕抂儌乕儊儞僩偲壸廳宯乮倐乯偺摍壙
丂丂丂丂愡揰壸廳偑僉儍儞僙儖偝傟丆拞娫壸廳偺傒偑晹嵽偵嶌梡偟偨晹嵽墳椡偑媮傑傞丅
丂丂丂丂丂丂丂丂丂嬶懱揑側寁嶼椺乣僥僉僗僩倫67偺椺戣3傪嶲徠偺偙偲丅
偙偺儁乕僕偺愭摢傊栠傞
乮2乯丂懡尦楢棫侾師曽掱幃偺夝朄
丂峔憿暔偺惷揑夝愅偱偼丆嵟廔揑偵師偺宍偺懡尦楢棫侾師曽掱幃傪夝偔偙偲偵側傞丅
丂丂丂丂丂丂丂丂丂丂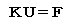 丂丂丂丂
丂丂丂丂
丂丂丂偙偙偱丆丂K丗崉惈儅僩儕僢僋僗乮晹嵽僨乕僞摍偑梌偊傜傟傞偲丆妋掕乯
丂丂丂丂丂丂丂丂 U丗曄埵儀僋僩儖乮枹抦乯
丂丂丂丂丂丂丂 丂F丗壸廳儀僋僩儖乮奜椡偑梌偊傜傟傞偲丆妋掕乯
丂丂懡尦楢棫侾師曽掱幃偺夝朄偵偼丆戝偒偔捈愙夝朄偲斀暅夝朄偑偁傞丅偙偙偱偼丆捈愙夝朄
丂偺婎杮偱偁傞Gauss偺徚嫀朄偵偮偄偰夝愢偡傞丅
Gauss偺徚嫀朄偺寁嶼椺
丂師偺係尦偺娙扨側楢棫曽掱幃傪Gauss偺徚嫀朄偱夝偔丅
丂丂丂丂丂丂丂丂丂丂丂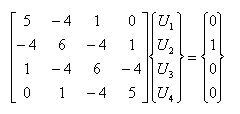
丂乮1乯慜恑徚嫀丂丗丂忋嶰妏儅僩儕僢僋僗偵曄宍偡傞庤懕偒
丂丂丂僗僥僢僾丂1丂丗丂戞1峴偺懳妏梫慺傛傝壓偺戞1楍梫慺偑慡偰0偲側傞傛偆偵丆師偺幃傪
丂丂丂丂丂丂丂丂丂丂丂丂丂梡偄偰曄宍偡傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂乮倝丆倞乯梫慺亅乷乮倝丆侾乯梫慺/乮侾丆侾乯偺懳妏梫慺乸亊乮1丆倞乯梫慺
丂丂丂丂丂丂丂丂丂丂丂丂丂丂偙偙偵丆丂 倝亖2丆倞亖侾乣4
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 丂 倝亖3丆倞亖1乣4
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂倝亖4丆倞亖1乣4
丂丂丂丂丂丂丂丂丂丂丂丂丂丂偙偺偲偒丆壸廳儀僋僩儖傕摨條偵曄宍偡傞丅
丂丂丂丂丂丂丂丂丂丂丂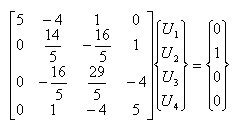
丂丂丂僗僥僢僾丂2丂丗丂戞2峴偺懳妏梫慺傛傝壓偺梫慺偑0偲側傞傛偆偵曄宍偡傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂曄宍偺峫偊曽偼丆忋婰偵摨偠乮埲壓摨條乯
丂丂丂丂丂丂丂丂丂丂丂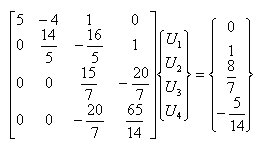
丂丂丂僗僥僢僾丂3丂丗丂戞3峴偺懳妏梫慺傛傝壓偺梫慺偑0偲側傞傛偆偵曄宍偡傞丅
丂丂丂丂丂丂丂丂丂丂丂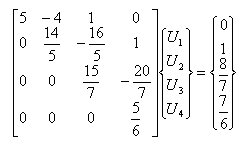
丂乮2乯屻戅戙擖丂丗丂嵟廔峴偺枹抦曄埵傪愭偢媮傔丆師偄偱乮嵟廔亅1乯峴丆丏丏丏俀丆1峴偺弴斣
丂丂丂丂丂丂丂丂丂丂丂丂偱枹抦曄埵傪媮傔傞庤懕偒
丂丂丂丂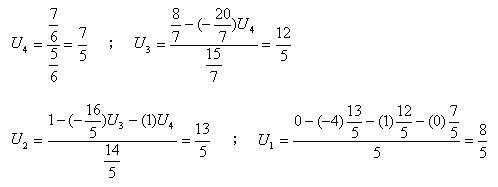
丂峔憿暔傪夝偔嵺偺崉惈儅僩儕僢僋僗偺摿挜
丂丂丒丂惓曽懳徧儅僩儕僢僋僗
丂丂丒丂庡懳妏梫慺偼慡偰惓偺抣傪偲傞
丂丂丒丂僶儞僪忬儅僩儕僢僋僗
丂丂
丂丂丂幚梡揑側僾儘僌儔儉偼丆婎杮揑偵偼忋婰俧倎倳s倱偺徚嫀朄偺墳梡偱偁傞応崌偑懡偄偑丆
丂丂忋婰偺摿挜傪嵟戝尷偵棙梡偟偰丆岠棪偺椙偄墘嶼傗梕検偺愡栺傪幚尰偟偰偄傞丅
偙偺儁乕僕偺愭摢傊栠傞
乮3乯丂梫慺崉惈儅僩儕僢僋僗
丂掁崌儅僩儕僢僋僗丂H丂傪梡偄偨桿摫
丂乮1乯丂掁崌儅僩儕僢僋僗乮晹嵽抂壸廳偲晹嵽墳椡偺娭學乯
丂丂丂丂丂丂拞娫壸廳偺側偄晹嵽偺墳椡偼丆3偮偺撈棫側晹嵽抂壸廳偑寛傑傟偽慡偰掕傔傞
丂丂丂丂丂丂偙偲偑弌棃傞丅
丂丂丂丂丂丂丂丂丂晹嵽抂壸廳丂6屄丂丂丂丂丂乣丂1愡揰摉偨傝3帺桼搙亊2愡揰乮1抂偲2抂乯
丂丂丂丂丂丂丂丂丂晹嵽偺掁崌忦審幃丂3屄丂乣丂倶曽岦丆倷曽岦丆儌乕儊儞僩偺椡偺掁崌
丂丂丂丂丂丂晹嵽偺掁崌忦審幃傪峫椂偡傞偲丆晹嵽抂壸廳6屄偺撪偺3屄偼廬懏揑偵掕傑傞丅
丂丂丂丂丂椺偊偽丆壓恾偺傛偆偵2抂懁傪晹嵽墳椡偵懳墳偡傞撈棫側3屄偺晹嵽抂壸廳偲壖掕
丂丂丂丂丂偡傞偲丆恾傛傝倫倶2亖倲丆倫倷2亖亅倯丆倣2偼晹嵽抂儌乕儊儞僩偵摨偠偲側傞丅1抂懁偼晹嵽
丂丂丂丂丂偺掁崌忦審偐傜掕傑傞廬懏揑側壸廳偲側傞丅偙傟偼晹嵽傪1抂偱屌掕偝傟偨曅帩偪椑
丂丂丂丂丂偲傒側偡偙偲偵憡摉偡傞丅
丂丂丂丂丂丂丂丂丂丂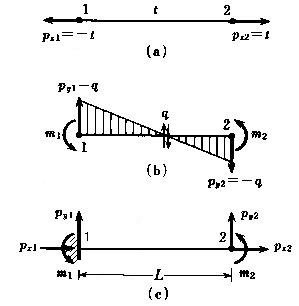
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂恾丂3-1丂晹嵽抂壸廳偲晹嵽抂墳椡偲偺娭學
丂丂丂丂丂丂丂丂丂1抂偺廬懏側晹嵽抂壸廳偼丆晹嵽偺掁崌忦審幃丆懄偪倶曽岦丆倷曽岦偺椡偺
丂丂丂丂丂丂丂丂掁崌幃偲1抂夢傝偺儌乕儊儞僩偺掁崌幃偐傜師偺傛偆偵媮傔傜傟傞丅
丂丂丂丂丂丂丂丂丂丂丂丂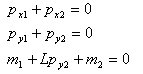
丂丂丂丂丂丂丂丂偙傟傪儅僩儕僢僋僗昞帵偡傞偲丆
丂丂丂丂丂丂丂丂丂丂丂丂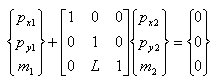
丂丂丂丂丂丂丂丂偝傜偵丆忋幃傪娙寜偵婰弎偡傞偲丆師偺傛偆偵昞偝傟傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂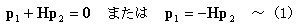
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂偙偙偵丆H丗掁崌儅僩儕僢僋僗
丂乮2乯丂晹嵽偺曄宍儀僋僩儖乮晹嵽曄宍偲崉懱曄埵乯
丂丂丂丂丂丂捠忢丆晹嵽抂偺曄埵偵偼椉晹嵽抂偺憡懳曄埵偲晹嵽偺崉懱曄埵偑娷傑傟傞丅懄偪丆
丂丂丂丂丂丂丂丂丂晹嵽抂偺曄埵亖椉晹嵽抂偺憡懳曄埵亄晹嵽偺崉懱曄埵
丂丂丂丂丂丂丂椉晹嵽抂偺憡懳曄埵偺偙偲傪晹嵽曄宍偲屇傇丅
丂丂丂丂丂丂偙傟傪恾偱帵偡偲丆師偺傛偆偵昞偝傟傞丅
丂丂丂丂丂丂丂丂丂丂丂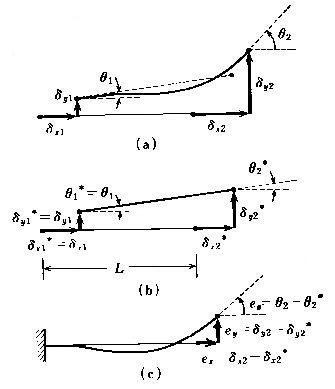
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂恾丂3-2丂晹嵽曄宍偲崉懱曄埵
丂丂丂丂丂丂晹嵽偺崉懱曄埵偺掕媊丂丗丂崉懱曄埵偼晹嵽抂曄埵偵*傪晅偗偰昞偡丅
丂丂丂丂丂丂丂丂丂丂丂丂丂1抂偺崉懱曄埵偼丆晹嵽抂曄埵偵摨偠偲掕媊偡傞丅丂懄偪丆丂倓1*亖倓1
丂丂丂丂丂丂丂丂丂丂丂丂丂2抂偱偼丆1抂偲2抂偺崉懱曄埵偵偮偄偰師偺娭學
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂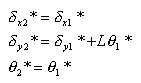
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂偑偁傝丆偙傟傪儅僩儕僢僋僗昞帵偡傞偲丆
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂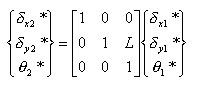
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂娙寜偵婰弎偡傞偲丆師偺傛偆偵昞偝傟傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂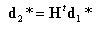
丂丂丂丂丂丂椉晹嵽抂娫偺憡懳曄埵乮晹嵽曄宍乯丂丗丂
丂丂丂丂丂丂丂丂丂丂丂丂丂忋恾乮們乯偺2抂偺曄埵偑丆椉晹嵽抂娫偺憡懳曄埵丆懄偪晹嵽曄宍傪昞偟丆
丂丂丂丂丂丂丂丂丂丂丂丂丂師偺幃偱昞偝傟傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂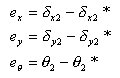
丂丂丂丂丂丂丂丂丂丂丂丂丂娙寜偵婰弎偡傞偲丆
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂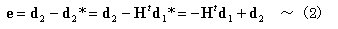
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂偙偙偵丆倕丂丗晹嵽曄宍儀僋僩儖
丂丂丂丂丂丂丂丂丂丂丂丂丂丂偟偨偑偭偰丆晹嵽曄宍儀僋僩儖倕偼丆晹嵽抂曄埵倓1丆倓2偐傜寁嶼偱偒傞丅
丂乮3乯丂梫慺崉惈儅僩儕僢僋僗乮晹嵽抂壸廳乣晹嵽抂曄埵丂娭學乯
丂丂丂丂丂丂恾3-2(c)恾傛傝丆晹嵽曄宍儀僋僩儖倕偺奺梫慺偼丆師偺恾偵帵偡傛偆偵2抂偵撈棫側
丂丂丂丂丂晹嵽抂壸廳傪庴偗傞曅帩偪椑偺曄宍偲偟偰寁嶼偱偒傞丅
丂丂丂丂丂丂丂慜採忦審丗晹嵽偼摍抐柺捈慄嵽偲壖掕偟丆偣傫抐曄宍偼峫椂偟側偄丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂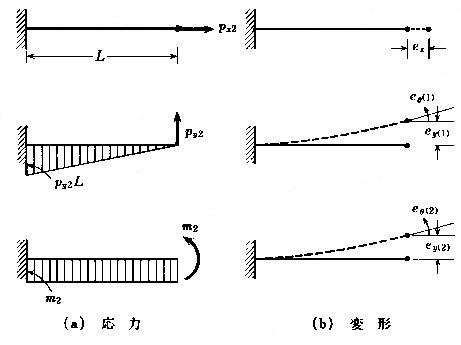
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂恾丂3-3丂愭抂壸廳傪庴偗傞曅帩偪偽傝偺墳椡偲曄宍
丂丂丂丂丂丂丂幉曽岦椡倫倶2偵傛傞嵽幉曄宍倕倶丆偍傛傃晹嵽抂壸廳倫倷俀丆倣2偵傛傞潥傒偲夞揮妏偼丆
丂丂丂丂丂丂師偺傛偆偵媮傔傜傟傞丅
丂丂丂丂丂丂丂丂丂丂丂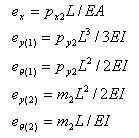
丂丂丂丂丂丂丂丂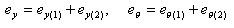
丂丂丂丂丂丂丂丂偱偁傞偙偲傪峫椂偡傞偲丆師偺娭學幃偑摼傜傟傞丅
丂丂丂丂丂丂丂丂丂丂丂丂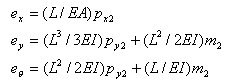
丂丂丂丂丂丂丂偙傟傪儅僩儕僢僋僗昞帵偡傞偲丆
丂丂丂丂丂丂丂丂丂丂丂丂丂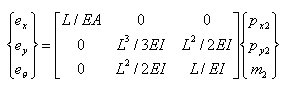
丂丂丂丂丂丂丂娙寜偵昞帵偡傞偲丆
丂丂丂丂丂丂丂丂丂丂丂丂丂丂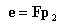
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂偙偙偵丆俥丗潥傒惈儅僩儕僢僋僗乮flexibility matrix乯
丂丂丂丂丂丂丂堦曽丆忋偺幃傪晹嵽抂壸廳偵偮偄偰夝偒丆儅僩儕僢僋僗昞帵偡傞偲丆
丂丂丂丂丂丂丂丂丂丂丂丂丂丂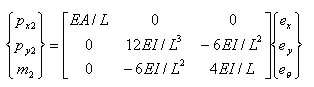
丂丂丂丂丂丂丂娙寜偵昞帵偡傞偲丆
丂丂丂丂丂丂丂丂丂丂丂丂丂丂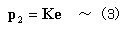
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂偙偙偵丆俲丗崉惈儅僩儕僢僋僗乮stiffness matrix乯
丂丂丂丂丂丂丂潥傒惈儅僩儕僢僋僗丆崉惈儅僩儕僢僋僗偼懳徧儅僩儕僢僋僗偱屳偄偵媡儅僩儕僢僋僗偺
丂丂丂丂丂丂娭學偵偁傞丅
丂丂丂丂丂丂晹嵽偺峔惉曽掱幃乮晹嵽抂壸廳乣晹嵽抂曄埵丂娭學乯偼丆崉惈儅僩儕僢僋僗傪梡偄傞
丂丂丂丂丂偲師偺幃偱昞尰偱偒傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂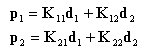
丂丂丂丂丂丂偙傟傪儅僩儕僢僋僗昞帵偡傞偲丆
丂丂丂丂丂丂丂丂丂丂丂丂丂丂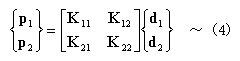
丂丂丂丂丂丂埲忋偱丆嬶懱揑側峔惉曽掱幃傪帵偡弨旛偑惍偭偨丅
丂丂丂丂丂丂忋偺3偮偺幃丆乮1乯丆乮2乯丆乮3乯幃傪嵞搙暲傋偰婰偡偲丆
丂丂丂丂丂丂丂丂丂丂丂丂丂丂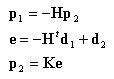
丂丂丂丂丂丂乮3乯幃傪乮1乯幃偵戙擖偟丆乮3乯幃偲暲婰偟丆偝傜偵乮2乯幃傪峫椂偟丆惍棟偡傞偲丆
丂丂丂丂丂丂丂丂丂丂丂丂丂丂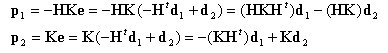
丂丂丂丂丂丂乮4乯幃偲忋幃傪斾妑偡傞偲丆
丂丂丂丂丂丂丂丂丂丂丂丂丂丂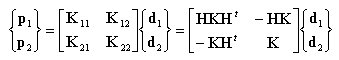
丂丂丂丂丂丂
丂丂丂丂丂丂嬶懱揑偵梫慺崉惈儅僩儕僢僋僗俲傪婰弎偡傞偲丆師偺傛偆偵昞偝傟傞丅
丂丂
丂丂丂丂丂丂偙偺幃偼丆晹嵽嵗昗宯偱昞帵偝傟偨晹嵽抂壸廳偲晹嵽抂曄埵傪娭學晅偗傞
丂丂丂丂丂丂梫慺崉惈儅僩儕僢僋僗偱偁傞丅
丂潥傒妏朄偺婎杮幃傪梡偄偨桿摫
丂丂慜採忦審丂丗丂旝彫曄宍棟榑偑惉棫偡傞
丂丂丂丂丂丂丂丂丂丂丂拞娫壸廳偑嶌梡偟側偄
丂丂丂丂丂丂丂丂丂丂丂幉曽岦椡偲嬋偘偲偼楢惉偟側偄丅
丂丂丂潥傒妏朄偺婎杮幃偼丆師偺捠傝偱偁傞丅
丂丂丂丂丂丂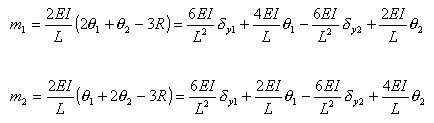
丂丂丂丂丂丂丂丂丂丂丂丂丂偨偩偟丆晹嵽妏丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂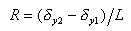
丂丂丂傑偨丆幉曽岦椡偲幉曽岦曄埵偺娭學偼丆慜採忦審偱嬋偘偲偺楢惉岠壥傪柍帇偟偰偄傞
丂丂丂偺偱丆師偺傛偆偵昞偝傟傞丅
丂丂丂丂丂丂丂丂丂丂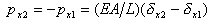
丂丂丂偝傜偵丆偣傫抐椡偼丆拞娫壸廳偑嶌梡偟側偄偲偟偰偄傞偺偱丆椉抂偺嬋偘儌乕儊儞僩偐傜
丂丂丂師幃偱摼傜傟傞丅
丂丂丂丂丂丂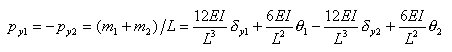
丂丂丂埲忋偺幃傪儅僩儕僢僋僗昞帵偡傞偲丆埲壓偺傛偆偵側傞丅
丂丂丂
丂丂丂偙偺幃偼丆晹嵽嵗昗宯偱昞帵偝傟偨晹嵽抂壸廳偲晹嵽抂曄埵傪娭學晅偗傞曽掱幃偱偁傞丅
丂丂婎弨嵗昗宯昞帵傊偺曄姺
丂丂丂丂丂丂晹嵽嵗昗宯偱昞帵偝傟偨梫慺崉惈儅僩儕僢僋僗傪婎弨嵗昗宯偵曄姺偡傞偵偼丆
丂丂丂丂丂嵗昗曄姺儅僩儕僢僋僗傪梡偄傞丅
丂丂丂丂丂丂丂晹嵽嵗昗宯偱昞帵偝傟偨晹嵽抂壸廳偲晹嵽抂曄埵偺娭學幃偼丆
丂丂丂丂丂丂丂丂丂丂丂丂丂丂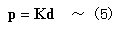
丂丂丂丂丂丂丂崪慻峔憿夝愅偺婎慴丆嵗昗曄姺儅僩儕僢僋僗偺崁偵偍偄偰桿摫偟偨幃傪嵞宖偡傞偲丆
丂丂丂丂丂丂丂丂丂丂丂丂丂丂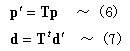
丂丂丂丂丂丂丂偱偁傞丅乮5乯幃偺椉曈偵俿傪嵍忔愊偟丆乮7乯幃傪戙擖偡傞偲
丂丂丂丂丂丂丂丂丂丂丂丂丂丂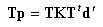
丂丂丂丂丂丂丂偝傜偵丆乮6乯幃傪峫椂偡傞偲
丂丂丂丂丂丂丂丂丂丂丂丂丂丂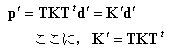
丂丂丂丂丂丂丂丂俲乫偼婎弨嵗昗宯偱昞帵偟偨梫慺崉惈儅僩儕僢僋僗偱偁傞丅
丂丂丂丂丂丂丂偨偩偟丆偙傟偼晹嵽抂壸廳乣晹嵽抂曄埵丂娭學乮婎弨嵗昗宯昞帵乯偱偁傞丅
丂丂丂丂丂丂丂愡揰壸廳乣愡揰曄埵娭學乮婎弨嵗昗宯昞帵乯傊偺抲偒姺偊偵偮偄偰偼丆揔崌忦審丆
丂丂丂丂丂丂丂掁崌忦審偺崁嶲徠偺偙偲丅
丂偙偺儁乕僕偺愭摢傊栠傞
乮4乯丂掁崌忦審丆揔崌忦審
丂丂掁崌忦審
丂丂丂丂丂掁崌忦審偼丆愡揰偵偍偗傞椡偺掁崌忦審傪堄枴偟丆乭愡揰壸廳偼偦偺愡揰偵愙懕偟偰
丂丂丂丂偄傞晹嵽抂壸廳乮婎弨嵗昗宯偱昞帵乯偺榓偵摍偟偄乭丂偙偲傪昞偟偨師偺幃偱昞尰偝傟傞丅
丂丂丂丂丂丂丂丂丂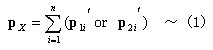
丂丂丂丂丂丂偨偩偟丆倝丂偼愡揰倃丂偵愙懕偡傞晹嵽柤
丂丂丂丂丂丂丂丂丂丂丂値丂偼愡揰倃丂偵愙懕偡傞晹嵽悢
丂丂丂丂丂嬶懱椺
丂丂丂丂丂丂丂丂丂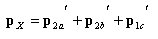
丂丂揔崌忦審
丂丂丂丂丂揔崌忦審偼丆愡揰偵偍偗傞曄埵偺揔崌忦審傪堄枴偟丆乭愡揰曄埵偼偦偺愡揰偵愙懕
丂丂丂丂偟偰偄傞晇乆偺晹嵽抂曄埵乮婎弨嵗昗宯偱昞帵乯偵摍偟偄乭丂偙偲傪昞偟偨師偺幃偱昞尰
丂丂丂丂偝傟傞丅
丂丂丂丂丂丂丂丂丂丂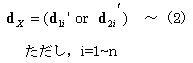
丂丂丂丂丂嬶懱椺
丂丂丂丂丂丂丂丂丂丂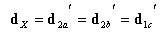
丂丂愡揰壸廳乣愡揰曄埵娭學偺崉惈儅僩儕僢僋僗傊偺抲偒姺偊
丂丂丂慜採忦審丗愡揰偲晹嵽抂偺娫偵崉堟偼懚嵼偟側偄偲偡傞丅
丂丂丂晹嵽抂壸廳乣晹嵽抂曄埵偺娭學偼梫慺崉惈儅僩儕僢僋僗偺崁偱婎弨嵗昗宯昞帵偺応崌丆
丂丂丂師偺傛偆偵媮傔傜傟偨丅
丂丂丂丂丂丂丂丂丂丂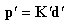
丂丂丂忋幃偑丂倝丂晹嵽偵偮偄偰偺娭學幃偱偁傞偲峫偊傞偲丆
丂丂丂丂丂丂丂丂丂丂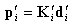 丂丂丂
丂丂丂
丂丂丂懄偪丆
丂丂丂丂丂丂丂丂丂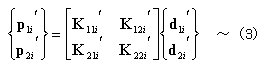
丂丂丂偙傟傪愡揰壸廳乣愡揰曄埵娭學乮婎弨嵗昗宯昞帵乯偵抲偒姺偊傞偵偼丆忋婰偺掁崌忦審
丂丂丂幃偲揔崌忦審幃傪梡偄傞丅揔崌忦審幃傛傝丆i晹嵽偺曅曽偺抂晹偼愡揰倃偵愙懕偡傞偲
丂丂丂壖掕偡傞偲丆晹嵽抂曄埵偺偄偢傟偐堦曽乮倓侾倝乫傑偨偼倓俀倝乫乯偼愡揰曄埵倓倶偵摍偟偄丅
丂丂丂懄偪丆
丂丂丂丂丂丂丂丂丂丂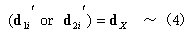
丂丂丂愡揰壸廳俹倶偼愡揰倃偵愙懕偡傞暋悢晹嵽偺愡揰壸廳婑梌暘偺榓偵摍偟偄偲傕夝庍偱
丂丂丂偒傞偺偱丆倝丂晹嵽偐傜偺愡揰壸廳婑梌暘傪俹X1i傑偨偼俹X2i偲抲偔偲丆
丂丂丂丂丂丂丂丂丂丂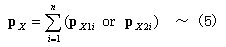
丂丂丂忋幃偲掁崌忦審乮1乯幃偲偺斾妑偐傜丆
丂丂丂丂丂丂丂丂丂丂丂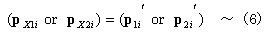
丂丂丂偲抲偗傞丅倝丂晹嵽偺1抂偑愡揰倃偵愙懕偟丆2抂偑愡揰倅偵愙懕偡傞偲壖掕偡傞偲丆乮4乯丄
丂丂丂乮6乯幃偐傜乮3乯幃偼寢嬊師偺傛偆偵愡揰壸廳乣愡揰曄埵娭學偱昞帵偝傟傞丅
丂丂丂丂丂丂丂丂丂丂丂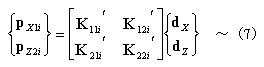
丂丂丂埲忋偺偙偲傛傝丆婎弨嵗昗宯偱昞帵偟偨晹嵽抂壸廳乣晹嵽抂曄埵娭學偺崉惈儅僩儕僢僋僗
丂丂丂偼丆愡揰壸廳乣愡揰曄埵娭學偺崉惈儅僩儕僢僋僗偵堦抳偡傞偙偲偑暘偐傞丅乮偨偩偟丆晹嵽
丂丂丂抂偲愡揰偺娫偵崉堟偑懚嵼偡傞応崌偼堦抳偟側偄乯
丂丂丂丂乮7乯幃偐傜暘偐傞傛偆偵丆愡揰壸廳乣愡揰曄埵娭學偺崉惈儅僩儕僢僋僗偼丆晹嵽丂倝丂偑
丂丂丂愙懕偡傞愡揰乮偙偺椺偱偼倃偲倅乯偵娭楢偡傞崉惈儅僩儕僢僋僗偱偁傞丅懄偪丆壓恾偺傛偆偵
丂丂丂晹嵽抂壸廳乣晹嵽抂曄埵娭學偺偲偒偵偼梫慺崉惈儅僩儕僢僋僗偼僐儞僷僋僩偵媗傑偭偰偄偨
丂丂丂偑丆慡懱崉惈儅僩儕僢僋僗傪嶌惉偡傞嵺偵偼丆愡揰壸廳乣愡揰曄埵娭學偵抲偒姺傢傞偺偱
丂丂丂愡揰偺暲傃偵墳偠偰攝抲偡傞昁梫偑偁傞丅丂
丂丂丂丂丂丂丂丂丂丂丂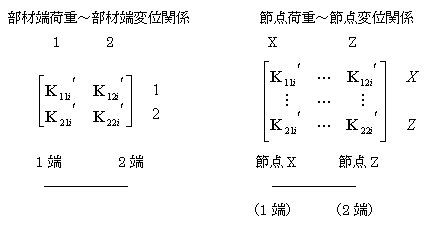
丂丂丂丂丂掁崌忦審偲揔崌忦審偼丆屄乆偺梫慺崉惈儅僩儕僢僋僗乮婎弨嵗昗宯昞帵乯偐傜崪慻
丂丂丂丂慡懱偺崉惈儅僩儕僢僋僗傪慻傒棫偰傞嵺偺埵抲寛傔偩偗偵娭梌偟偰偄傞丅
丂梫慺崉惈儅僩儕僢僋僗偺傑偲傔
丂丂丂崉惈偺掕媊丂乣丂扨埵潥傒傪堷偒婲偙偡偨傔偵昁梫側椡
丂丂丂潥傒惈偺掕媊乣扨埵壸廳偵傛傝惗偢傞潥傒
丂丂丂崉惈儅僩儕僢僋僗偺摿挜
丂丂丂丂丂丒丂懳徧儅僩儕僢僋僗偲側傞乮懄偪丆憡斀惈傪桳偡傞乯
丂丂丂丂丂丒丂崉惈儅僩儕僋僢僗偺庡懳妏梫慺偼惓偱偁傞乮椡偺岦偒偲媡曽岦偵曄埵偼惗偠側偄乯
丂丂丂丂丂丒丂晹嵽抂壸廳乣晹嵽抂曄埵娭學幃偍傛傃愡揰壸廳乣愡揰曄埵娭學幃偺奺峴偱偼丆
丂丂丂丂丂丂丂椡偺掁崌曽掱幃偑惉棫偟偰偄傞丅乮墘廗栤戣6嶲徠偺偙偲乯
丂丂
丂丂憡斀惈乮reciprocity乯
丂丂丂丂丂慄宍抏惈嫇摦偡傞峔憿暔偵懳偟偰偼廳偹崌傢偣偺尨棟偑惉棫偟丆潥傒惈學悢
丂丂丂丂乮潥傒惈儅僩儕僢僋僗偺奺梫慺乯偲崉惈學悢乮崉惈儅僩儕僢僋僗偺奺梫慺乯偲偼丆憡斀惈傪
丂丂丂丂桳偡傞乮倖倝倞=fji偍傛傃kij=kji乯丅
丂丂丂憡斀惈偺徹柧
丂丂丂丂壓恾偵帵偡峔憿暔偵丆師偺2捠傝偺弴彉偱壸廳偑嶌梡偡傞応崌偺巇帠乮榗僄僱儖僊乕乯
丂丂丂丂偵偮偄偰峫偊傞丅
丂丂丂丂丂丂乮1乯丂嵟弶偵壸廳F1偑丆師偵壸廳F2偑嶌梡偡傞応崌丒丒丒丒偙偺偲偒偺巇帠傪WI偱昞偡
丂丂丂丂丂丂乮2乯丂嵟弶偵壸廳F2偑丆師偵壸廳F1偑嶌梡偡傞応崌丒丒丒丒偙偺偲偒偺巇帠傪WII偱昞偡
丂丂丂丂丂丂丂丂丂丂丂丂丂丂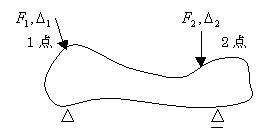
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂恾丂4-1丂憡斀惈
丂丂丂丂丂丂乮1乯偺弴彉偱壸廳傪嶌梡偝偣偨応崌偺巇帠偼丆壸廳F1偵懳偟偰丆
丂丂丂丂丂丂
丂丂丂丂丂丂丂偙偙偱丆F1傪堦掕偵曐偪F2傪嶌梡偝偣傞偲丆偦偺偲偒偺巇帠偼丆
丂丂丂丂丂丂丂丂丂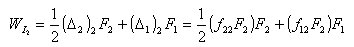
丂丂丂丂丂丂丂偟偨偑偭偰丆慡巇帠WI丂偼師偺傛偆偵側傞丅
丂丂丂丂丂丂丂丂丂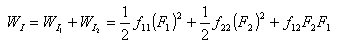
丂丂丂丂丂丂堦曽丆椡偺嶌梡弴彉傪媡偵乮2乯偱帵偟偨捠傝偵偟偰巇帠傪峫偊傞偲丆壸廳F2偵懳偟偰丆
丂丂丂丂丂丂丂丂丂丂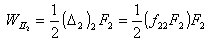
丂丂丂丂丂丂丂丂偙偙偱丆F2傪堦掕偵曐偪F1傪嶌梡偝偣傞偲丆偦偺偲偒偺巇帠偼丆
丂丂丂丂丂丂丂丂丂丂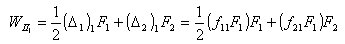
丂丂丂丂丂丂丂偟偨偑偭偰丆慡巇帠WII丂偼師偺傛偆偵側傞丅
丂丂丂丂丂丂丂丂丂丂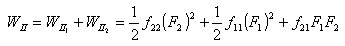
丂丂丂丂丂丂丂壸廳偑嶌梡偡傞弴彉偼慄宍宯偱偼側偝傟傞巇帠偵娭學偟側偄偺偱丆W偵娭偡傞
丂丂丂丂丂丂丂忋偺2偮偺幃傪摍偟偄偲抲偗傞偺偱丆師幃傪摼傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂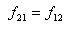
丂丂丂丂丂丂丂堦斒宍偱偼丆
丂丂丂丂丂丂丂丂丂丂丂丂丂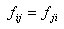
丂丂丂丂丂丂丂偙傟偼儅僢僋僗僂僃儖偺憡斀掕棟乮Maxwell's reciprocal theorem乯偲偟偰抦傜傟偰
丂丂丂丂丂丂丂偄傞傕偺偱偁傞丅
丂丂丂丂丂丂丂儅僢僋僗僂僃儖偺憡斀掕棟偼儀僢僥僀偺朄懃乮Betti's law乯偺摿庩側応崌偵憡摉丅
丂丂丂丂丂丂丂丂丂丂儀僢僥僀偺朄懃丂丗丂奜椡宯乷P2乸偵傛偭偰曄埵宯乷儮2乸偑惗偠偰偄傞偲偒偵丆
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂奜椡宯乷P1乸偵傛偭偰側偝傟傞巇帠偼丆乷P1乸偵傛偭偰乷儮1乸
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂偑惗偠偰偄傞偲偒偵丆乷P2乸偵傛偭偰側偝傟傞巇帠偵摍偟偄丅
丂丂丂丂丂丂丂丂丒丂潥傒惈儅僩儕僢僋僗偼懳徧儅僩儕僢僋僗偱偁傞丅
丂丂丂丂丂丂丂丂丒丂懳徧儅僩儕僢僋僗偺媡儅僩儕僢僋僗偼懳徧儅僩儕僢僋僗偱偁傞丅
丂丂丂丂丂丂丂丂丒丂潥傒惈儅僩儕僢僋僗偺媡儅僩儕僢僋僗偼崉惈儅僩儕僢僋僗偱偁傞丅
丂丂丂丂丂丂丂埲忋偺偙偲傛傝丆崉惈儅僩儕僢僋僗偼懳徧儅僩儕僢僋僗偱偁傞丅
丂丂丂丂丂丂丂懄偪丆
丂丂丂丂丂丂丂丂丂丂丂丂丂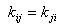
偙偺儁乕僕偺愭摢傊栠傞
丂乮5乯慡懱崉惈儅僩儕僢僋僗偺嶌惉
丂丂丂丂丂屄乆偺晹嵽偺梫慺崉惈儅僩儕僢僋僗乮婎弨嵗昗宯昞帵偺愡揰壸廳乣愡揰曄埵娭學乯傪
丂丂丂丂乮4乯掁崌忦審丆揔崌忦審偺崁偱弎傋偨晇乆偺埵抲寛傔偵偟偨偑偄攝抲偟偰丆崪慻慡懱
丂丂丂丂偺崉惈儅僩儕僢僋僗傪嶌惉偡傞丅
丂丂丂丂嬶懱椺偲偟偰丆3憌2僗僷儞偺師偺崪慻偵偮偄偰慡懱崉惈儅僩儕僢僋僗傪嶌惉偡傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂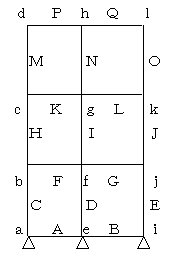
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂恾丂5-1丂3憌2僗僷儞崪慻
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮愡揰斣崋丆晹嵽斣崋乯
丂丂丂丂晹嵽偺梫慺崉惈儅僩儕僢僋僗乮婎弨嵗昗宯昞帵乯傪晹嵽柤傪倃偱戙昞偝偣偰昞偡偲
丂丂丂師偺傛偆偵側傞丅
丂丂丂丂丂丂丂丂丂丂丂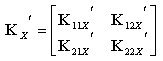
丂丂丂丂椺偊偽丆俙晹嵽偺応崌丆1抂丆2抂偼晇乆倎抂丆倕抂偵懳墳偟偰慡懱崉惈儅僩儕僢僋僗偵
丂丂丂攝抲偝傟傞丅
丂丂丂丂丂丂
丂丂丂丂埲壓丆摨條偵懠偺晹嵽偵偮偄偰傕椉抂偺愡揰斣崋偵墳偠偰慡懱崉惈儅僩儕僢僋僗偵
丂丂丂慻傒崬傑傟傞丅偙傟傪恾偵昞偡偲丆師偺傛偆偵側傞丅偨偩偟丆娙扨偺偨傔偵婎弨嵗昗宯傪
丂丂丂堄枴偡傞乫偼徣棯偟偨丅
丂丂丂丂丂丂丂丂丂丂丂倎丂丂丂丂丂丂丂丂丂丂丂倐丂丂丂丂丂丂丂丂丂丂丂丂丂們丂丂丂丂丂丂丂丂丂丂丂倓丂丂丂丂丂丂丂丂丂丂丂倕丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂倖丂
丂丂丂丂丂丂丂丂------------------------------------------------------------------------------------------------
丂丂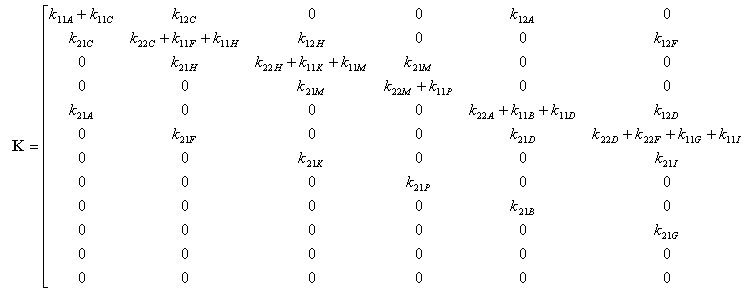
丂丂丂丂丂丂丂丂丂丂丂丂倗丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂倛丂丂丂丂丂丂丂丂丂丂倝丂丂丂丂丂丂丂丂丂丂丂丂倞丂丂丂丂丂丂丂丂丂丂丂丂丂倠丂丂丂丂丂丂丂丂丂丂丂倢
丂丂丂 -----------------------------------------------------------------------------------------------
丂丂丂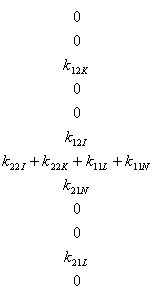 丂
丂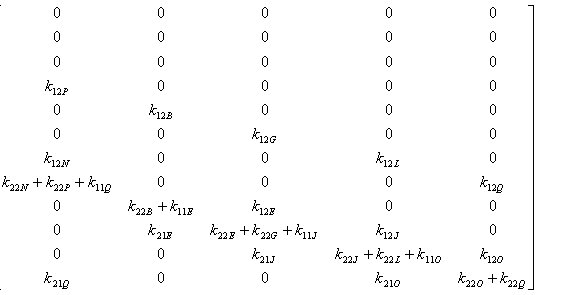
丂丂丂乮拲乯丂忋婰偺慡懱崉惈儅僩儕僢僋僗偺奺梫慺偼丆3亊3偺儅僩儕僢僋僗偱偁傞丅
丂嫬奅忦審乮boundary condition乯
丂丂丂丂嫬奅忦審偲偼丆峔憿暔偑奜揑偵峉懇偝傟丆曄埵偑婯掕偝傟偨抣偵嫮惂偝傟傞偙偲傪偄偆丅
丂丂丂忋偺儌僨儖偺応崌丆愡揰倎丆倕丆倝偺倃曽岦偲倄曽岦曄埵偑峉懇偝傟偰偍傝丆懡尦楢棫1師
丂丂丂曽掱幃傪夝偔慜偐傜奩摉曄埵偼0偱偁傞偙偲偑暘偐傞丅僥僉僗僩偱偼丆巟揰偵愙懕偡傞愡揰
丂丂丂壸廳丆愡揰曄埵偼懡尦楢棫1師曽掱幃偵娷傔側偄愢柧傪偟偰偄傞丅
丂丂丂丂偙傟偵偮偄偰偼丆僥僉僗僩倫84媟拲偵帵偝傟偨娙曋朄乮峉懇偝傟偰偄傞帺桼搙偵懳墳偡傞
丂丂丂庡懳妏梫慺偵戝偒側悢丆椺偊偽10偺20忔側偳傪妡偗偰丆奩摉曄埵偑嫮惂揑偵0偵尷傝側偔
丂丂丂嬤偔側傞傛偆偵偡傞乯傪梡偄傞偙偲偵傛傝丆巟揰偵愙懕偡傞愡揰壸廳丆愡揰曄埵傪懡尦楢棫
丂丂丂1師曽掱幃偵娷傔偨傑傑偱埖偆偙偲偑偱偒傞丅
丂丂丂丂側偍丆媟拲偺愢柧偱媅摿堎偲側偭偰悢抣寁嶼偑崲擄偵側傞偲偁傞偑丆偙傟偼幬傔
丂丂丂儘乕儔乕偺倷''曽岦偺傒偵娙曋朄傪揔梡偡傟偽丆夝寛偱偒傞丅
丂僒僽僗僩儔僋僠儍乕朄
丂丂丂丂偙偺庤朄偼丆夝愅懳徾偑戝婯柾偱偁傞偲偐嵶偐偔暘妱偟偰寁嶼偟偨偄応崌偵丆寁嶼婡
丂丂丂梕検偑彫偝夁偓偰捠忢偺曽朄偱偼丆寁嶼偑崲擄側応崌偵抦偭偰偄傞偲曋棙側曽朄偱偁傞丅
丂丂丂懄偪丆寁嶼僥僋僯僢僋偺傂偲偮偱偁傞丅
丂丂丂丂婎杮揑側峫偊曽偼丆晹暘峔憿乮Sub-Structure乯偲偟偰埖偊傞懳徾偵偮偄偰丆愡揰斣崋
丂丂丂傪晅斣偡傞嵺丆嫬奅揰乮懠偺晹嵽偵愙懕偡傞愡揰乯偲撪揰乮懠偺晹嵽偵愙懕偟側偄撪晹偺
丂丂丂愡揰乯偵暘偗偰峫偊傞丅師偵僒僽僗僩儔僋僠儍乕傪傂偲偮偺晹嵽埥偄偼梫慺偲峫偊丆崉惈儅僩
丂丂丂儕僢僋僗傪嶌惉偡傞丅偦偺嵺撪揰偐傜愡揰斣崋傪晅斣偟丆嫬奅揰偺愡揰偵偼慡偰偺撪揰偺
丂丂丂晅斣傪廔偊偰偐傜晅斣偡傞丅嵟屻偵撪揰偵娭偡傞崁偺傒徚嫀偟丆撪揰偺塭嬁傪斀塮偟偨
丂丂丂嫬奅揰偵娭偡傞崉惈儅僩儕僢僋僗傪媮傔傞丅偙偺憖嶌傪弅栺偲屇傃丆弅栺屻偺崉惈傪
丂丂丂僗乕僷乕僄儗儊儞僩偺崉惈偲屇傇応崌傕偁傞丅崪慻慡懱偺崉惈儅僩儕僢僋僗傪慻傒棫偰傞嵺
丂丂丂偵偼丆僒僽僗僩儔僋僠儍乕偵娭偟偰偼弅栺屻偺崉惈傪摉偰傞丅
丂丂丂丂楢棫堦師曽掱幃傪夝偄偰嫬奅揰偺曄埵偑媮傑偭偨傜丆偦傟傪婎偵撪揰偺曄埵傪媮傔傞丅
丂丂丂忋婰偵娭楢偡傞幃偺揥奐偼丆暿搑島媊帪偵徯夘偡傞丅
偙偺儁乕僕偺愭摢傊栠傞
丂乮6乯丂偣傫抐曄宍丆崉堟偍傛傃嵽抂夞揮偽偹偺庢傝埖偄
丂偣傫抐曄宍傪峫椂偟偨崉惈儅僩儕僢僋僗
丂丂丂丂師偺摍抐柺捈慄嵽偺恾偵偍偄偰丆椡偺掁崌幃傪偨偰傞偲師偺傛偆偵側傞丅
丂丂丂丂丂丂丂丂丂丂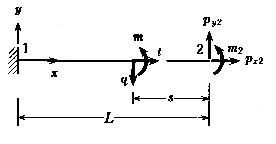
丂丂丂丂丂丂丂丂丂丂丂丂丂恾丂6-1丂摍抐柺捈慄嵽
丂丂丂丂丂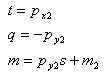
丂丂丂偙傟傪榗僄僱儖僊乕幃偵戙擖偡傞偲丆
丂丂丂丂丂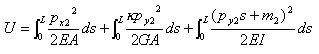
丂丂丂忋幃傪愊暘偡傞偲丆師偺幃偑摼傜傟傞丅
丂丂丂丂丂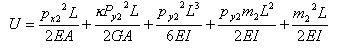
丂丂丂師偵丆僇僗僠儕傾乕僲偺戞擇掕棟傛傝丆榗僄僱儖僊乕傪壸廳偱曃旝暘偟曄宍傪媮傔傞偲丆
丂丂丂丂丂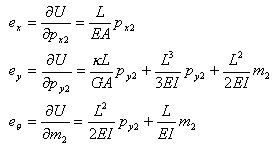
丂丂丂埲忋傪傑偲傔偰儅僩儕僢僋僗昞帵偡傞偲丆師偺傛偆偵側傞丅
丂丂丂丂丂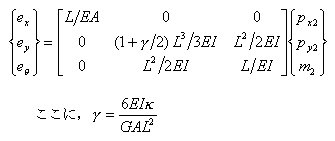
丂丂丂偙傟傪娙寜偵昞帵偡傞偲丆
丂丂丂丂丂丂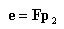
丂丂丂潥傒惈儅僩儕僢僋僗俥偺幃拞兞/2偼嬋偘曄宍偵懳偡傞偣傫抐曄宍偺斾棪傪昞偡丅
丂丂丂崉惈儅僩儕僢僋僗俲偼俥偺媡儅僩儕僢僋僗偲偟偰丆媮傔傜傟傞丅
丂丂丂丂丂丂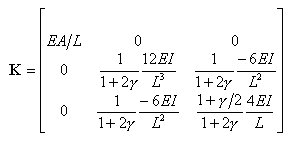
丂丂丂嶲峫丗媡儅僩儕僢僋僗偺寁嶼
丂丂丂丂丂丂丂丂丂
丂崉堟傪桳偡傞晹嵽偺崉惈儅僩儕僢僋僗
丂丂掁崌儅僩儕僢僋僗偺愊乮弨旛偦偺1乯
丂丂丂丂掁崌儅僩儕僢僋僗俫偺摥偒
丂丂丂丂丂丒丂晹嵽偺掁崌忦審傪昞偡丅
丂丂丂丂丂丒丂晹嵽偺椉抂偺崉懱曄埵偺娭學傪昞偡丅
丂丂丂丂丂丂丂丂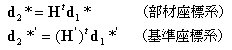
丂丂丂掁崌儅僩儕僢僋僗偺愊乣2偮偺晹嵽偑壓恾偵帵偡傛偆偵崉偵愙崌偝傟丆晹嵽偵拞娫壸廳偑
丂丂嶌梡偟偰偄側偗傟偽丆2晹嵽倎丆倐偐傜惉傞晹嵽傪1晹嵽們偲尒側偡偲偒丆
丂丂們晹嵽偺掁崌儅僩儕僢僋僗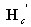 偼倎晹嵽偲倐晹嵽偺掁崌儅僩儕僢僋僗
偼倎晹嵽偲倐晹嵽偺掁崌儅僩儕僢僋僗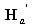 丂偲
丂偲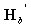 丂偺愊偱
丂偺愊偱
丂丂梌偊傜傟傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂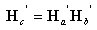
丂丂丂丂丂丂丂丂丂丂丂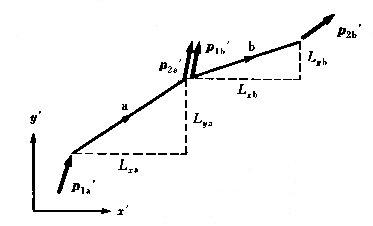
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂恾丂6-2丂崉愙2晹嵽偐傜惉傞晹嵽
丂丂丂乮徹柧乯
丂丂丂丂丂丂倎晹嵽偵偮偄偰椉抂偺崉懱曄埵偺娭學偼丆
丂丂丂丂丂丂丂丂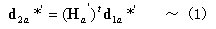
丂丂丂丂丂丂倐晹嵽偵偮偄偰摨條偵
丂丂丂丂丂丂丂丂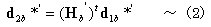
丂丂丂丂丂丂揔崌忦審傛傝丆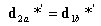 偱偁傞偐傜丆偙偺娭學傪峫椂偟偰乮2乯幃偵乮1乯幃傪
偱偁傞偐傜丆偙偺娭學傪峫椂偟偰乮2乯幃偵乮1乯幃傪
丂丂丂丂丂丂戙擖偡傞偲丆
丂丂丂丂丂丂丂丂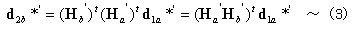
丂丂丂丂丂丂堦曽丆
丂丂丂丂丂丂丂丂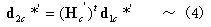
丂丂丂丂丂丂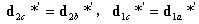 偱偁傞偐傜丆乮4乯幃傪峫椂偡傞偲乮3乯幃偼師偺
偱偁傞偐傜丆乮4乯幃傪峫椂偡傞偲乮3乯幃偼師偺
丂丂丂丂丂丂傛偆偵昞偣傞丅
丂丂丂丂丂丂丂丂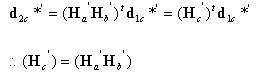
丂丂丂丂丂丂忋幃偼晹嵽偑3偮埲忋偺応崌偵懳偟偰傕奼挘偱偒丆
丂丂丂丂丂丂丂丂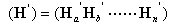
丂丂丂丂丂丂偲昞偡偙偲偑偱偒傞丅
丂丂捈楍楢嵔嵽偺崉惈儅僩儕僢僋僗乮弨旛偦偺2乯
丂丂丂壓恾偵帵偡傛偆偵捈楍楢嵔嵽偲偼丆悢屄偺摍抐柺捈慄嵽偑捈楍偵寢崌偝傟偨晹嵽傪偄偆丅
丂丂丂丂丂丂丂丂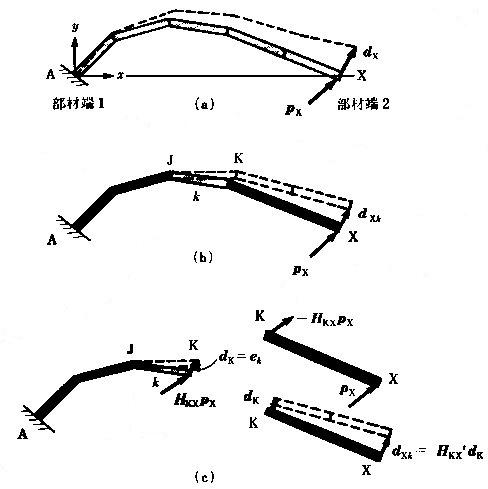
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂恾丂6-3丂捈楍楢嵔嵽偲梫慺倠偺榗偵傛傞曄宍
丂丂丂埲壓偵丆屄乆偺摍抐柺捈慄嵽偺潥傒惈儅僩儕僢僋僗偼婛抦偲壖掕偟丆捈楍楢嵔嵽俙倃
丂丂偺慡懱崉惈儅僩儕僢僋僗傪桿摫偡傞丅側偍丆埲壓偵偍偄偰偼丆曄埵丆壸廳丆掁崌儅僩儕僢僋僗丆
丂丂潥傒惈儅僩儕僢僋僗偼晹嵽俙倃慡懱偵偮偄偰嫟捠偺晹嵽嵗昗宯偱昞帵偝傟偰偄傞傕偺偲偡傞丅
丂丂倠晹嵽偺倃抂曄埵婑梌暘倓倃k偺嶼掕
丂丂丂鶣乯丂倠晹嵽俲抂偺曄埵倓俲偺寁嶼
丂丂丂丂丂丂丂丂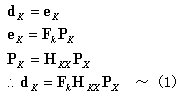
丂丂丂鶤乯丂俲倃晹暘偺曄埵
丂丂丂丂丂丂丂丂俲倃偺椉抂偺曄埵娫偵偼丆俲倃偼崉懱偩偐傜師幃偑惉棫偡傞丅
丂丂丂丂丂丂丂丂丂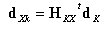
丂丂丂丂丂丂丂丂屘偵丆倠晹嵽偺婑梌偵傛傞倃抂偺曄埵偼丆
丂丂丂丂丂丂丂丂丂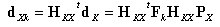
丂丂丂丂丂丂丂丂傛偭偰捈楍楢嵔嵽偑値屄偺摍抐柺捈慄嵽偐傜惉偭偰偄傞偲偡傞偲丆倓倃偼師幃偺
丂丂丂丂丂丂丂傛偆偵昞偝傟傞丅
丂丂丂丂丂丂丂丂丂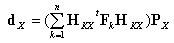
丂丂丂丂丂丂丂丂忋幃偺乮丂乯撪偑俙倃慡懱偲偟偰偺潥傒惈儅僩儕僢僋僗俥俙倃偱偁傞丅屘偵丆
丂丂丂丂丂丂丂丂丂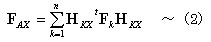
丂丂丂丂丂丂丂丂懄偪丆捈楍偵寢崌偝傟偨晹嵽偺潥傒惈儅僩儕僢僋僗偼丆屄乆偺晹嵽偺潥傒惈儅僩
丂丂丂丂丂丂丂儕僢僋僗俥k偵屻傠偐傜掁崌儅僩儕僢僋僗俫俲倃傪丆慜偐傜俫俲倃偺揮抲傪妡偗偰廋惓偟偨
丂丂丂丂丂丂丂傕偺偺榓偵摍偟偄丅崉惈儅僩儕僢僋僗俲俙倃偼俥俙倃傪媡曄姺偡傞偙偲偵傛傝媮傔傜傟傞丅
丂丂丂丂丂丂丂丂側偍丆偙偺崉惈儅僩儕僢僋僗偼捈楍楢嵔嵽傪惷掕婎杮晹嵽偲尒側偟偨偲偒偺崉惈
丂丂丂丂丂丂丂儅僩儕僢僋僗偱偁傞丅偟偨偑偭偰丆儅僩儕僢僋僗偺僒僀僘偼3亊3偱偁傞丅
丂丂丂丂丂丂丂丂晹嵽俙倃慡懱偵嫟捠偺晹嵽嵗昗宯昞帵偺峔惉曽掱幃偺崉惈儅僩儕僢僋僗偼丆僥僉
丂丂丂丂丂丂丂僗僩倫98偺乮3.24乯幃偵帵偡傛偆偵惷掕婎杮晹嵽偺崉惈儅僩儕僢僋僗俲俙倃偐傜媮傔傞丅
丂崉堟傪桳偡傞晹嵽偺崉惈儅僩儕僢僋僗偺桿摫
丂丂丂壓恾偺傛偆偵晹嵽偺椉抂偵崉堟傪桳偡傞応崌傪峫偊傞丅
丂丂丂丂丂丂丂丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂恾丂6-4丂崉堟傪桳偡傞晹嵽
丂丂丂崉堟傪桳偡傞応崌偼丆捈楍楢嵔嵽偺摿暿側応崌偲傒側偡偙偲偑偱偒傞偺偱丆乮2乯幃傛傝
丂丂丂俙俢晹嵽偺潥傒惈儅僩儕僢僋僗傪師偺傛偆偵昞帵偱偒傞丅
丂丂丂丂丂丂丂丂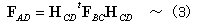
丂丂丂屘偵丆惷掕婎杮晹嵽偲偟偰偺崉惈儅僩儕僢僋僗偼丆
丂丂丂丂丂丂丂丂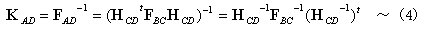
丂嶲峫丗媡峴楍偺婎杮岞幃
丂丂丂婎杮岞幃丂1丂丂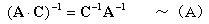
丂丂丂丂丂乮徹柧乯
丂丂丂丂丂丂丂丂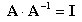 偵偍偄偰俙偺戙傢傝偵俙俠偲抲偔偲丆 偵偍偄偰俙偺戙傢傝偵俙俠偲抲偔偲丆
丂丂丂丂丂丂丂丂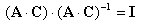
丂丂丂丂丂丂丂丂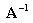 傪嵍忔愊偡傞偲丆 傪嵍忔愊偡傞偲丆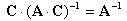
丂
丂丂丂丂丂丂丂丂峏偵 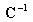 傪嵍忔愊偡傞偲丆 傪嵍忔愊偡傞偲丆
丂丂丂丂丂丂丂丂丂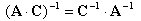
丂丂丂丂丂丂丂丂婎杮岞幃乮俙乯偼偝傜偵懡偔偺峴楍偺愊偵奼挘偱偒傞丅
丂丂丂丂丂丂丂丂丂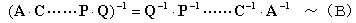
丂丂丂婎杮岞幃丂2丂丂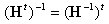
丂丂丂丂丂乮徹柧乯
丂丂丂丂丂丂丂丂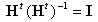 偺椉曈偵 偺椉曈偵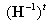 傪嵍忔愊偡傞偲 傪嵍忔愊偡傞偲
丂丂丂丂丂丂丂丂丂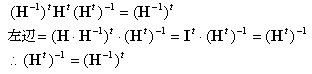
|
丂丂丂晹嵽嵗昗宯昞帵偺峔惉曽掱幃偼丆
丂丂丂丂丂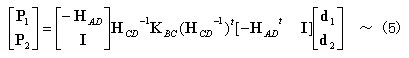
丂丂丂掁崌儅僩儕僢僋僗偺愊偺岞幃傛傝丆
丂丂丂丂丂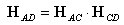
丂丂丂椉曈偵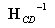 傪塃忔愊偡傞偲丆
傪塃忔愊偡傞偲丆
丂丂丂丂丂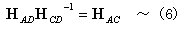
丂丂丂偝傜偵忋幃偺揮抲傪媮傔傞偲丆
丂丂丂丂丂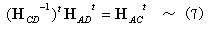
丂丂丂乮5乯幃偵偍偄偰乮6乯丆乮7乯幃傪峫椂偡傞偲丆
丂
丂丂丂
丂嵽抂偵夞揮偽偹傪桳偡傞晹嵽偺崉惈儅僩儕僢僋僗
丂丂丂壓恾偵帵偡傛偆偵丆嵽抂偵夞揮偽偹偑憓擖偝傟偨晹嵽偵偮偄偰峫偊傞丅嬶懱椺偲偟偰偼丆
丂丂丂揝崪憿偺椑抂偑僼傽僗僫乕傪夘偟偰儃儖僩偱拰偵愙崌偝傟偰偄傞応崌偵敿崉乮semi
-rigid乯
丂丂丂偺埖偄傪偟偰夝愅偡傞偙偲偑偁傞丅
丂丂丂丂丂丂丂丂丂丂丂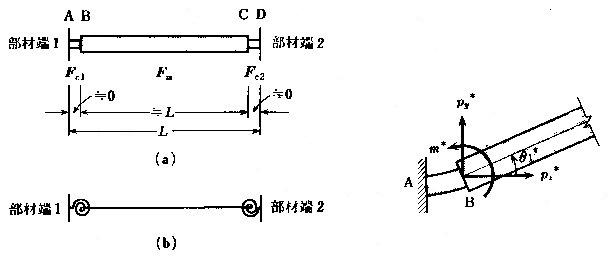
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂恾丂6-5丂嵽抂偵夞揮偽偹傪桳偡傞晹嵽丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂恾丂6-6丂夞揮偽偹偺曄宍
丂丂丂夞揮偽偹偑憓擖偝傟傞偙偲偵傛傝丆晹嵽偺曄宍偼師偺恾偵帵偡傛偆偵側傞丅懄偪丆
丂丂夞揮偽偹偺憓擖偵傛傝椉嵽抂偱夞揮妏偼晄楢懕偵儲俙丆儲D偩偗憹戝偡傞丅
丂丂丂丂丂丂丂丂丂丂丂丂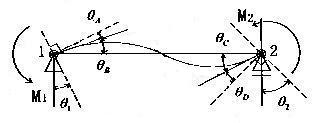
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂恾丂6-7丂晹嵽偺曄宍
丂丂丂偄傑丆1抂丆2抂偺夞揮偽偹偺崉惈傪師偺傛偆偵抲偗傞傕偺偲偡傞丅
丂丂丂丂丂丂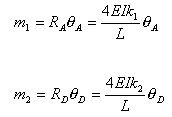
丂丂丂丂偙偙偱丆俼俙丆俼俢傪偦偺傑傑梡偄傞傛傝內1丆內2傪梡偄偨曽偑崉惈儅僩儕僢僋僗傪傛傝
丂丂丂娙寜側昞帵偵惍棟偡傞偙偲偑弌棃傞丅
丂丂丂丂恾丂6-6傪嶲徠偡傞偲丆俙俛晹暘偩偗傪庢傝弌偟偰俙抂傪屌掕偲偟偨偲偒偺俛揰懁偺
丂丂丂曄埵儀僋僩儖偼丆
丂丂丂丂丂丂丂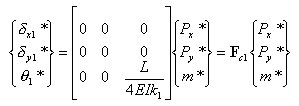
丂丂丂丂摨條偵俠俢晹暘偺潥傒惈儅僩儕僢僋僗俥俠2偼丆
丂丂丂丂丂丂丂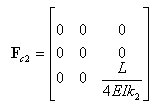
丂丂丂丂俛俠晹暘偺潥傒惈儅僩儕僢僋僗俥倣偼愭偵帵偟偨傛偆偵
丂丂丂丂丂丂丂丂
丂丂丂丂偟偨偑偭偰丆晹嵽慡懱偲偟偰偺潥傒惈儅僩儕僢僋僗偼乮2乯幃傪嶲徠偡傞偲丆
丂丂丂丂丂丂丂丂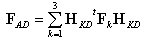
丂丂丂丂偲昞偡偙偲偑偱偒傞丅夞揮偽偹偺挿偝偼0偲壖掕偡傞偲丆師幃偑惉棫偡傞丅
丂丂丂丂丂丂丂丂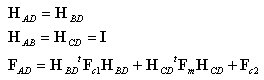
丂丂丂丂丂丂丂丂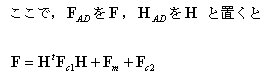
丂丂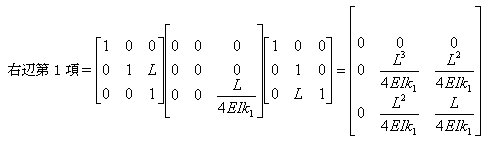
丂丂丂丂屘偵丆
丂丂丂丂丂丂丂丂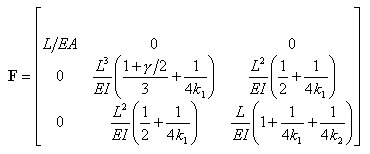
丂丂丂丂傛偭偰丆惷掕婎杮晹嵽偲偟偰偺崉惈儅僩儕僢僋僗偼丆
丂丂丂丂丂丂丂丂丂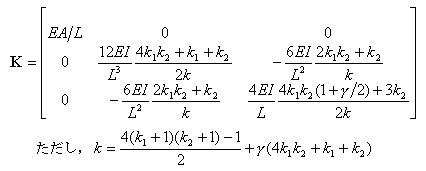
丂丂丂丂晹嵽嵗昗宯昞帵偺峔惉曽掱幃偺崉惈儅僩儕僢僋僗偼丆僥僉僗僩倫98偺乮3.24乯幃偵側傜偄
丂丂丂媮傔傞偙偲偑偱偒傞丅
丂丂丂丂丂側偍丆潥傒妏朄偺婎杮幃傪梡偄偨嵽抂偵夞揮偽偹傪桳偡傞晹嵽偺崉惈儅僩儕僢僋僗
丂丂丂丂乮偨偩偟丆偣傫抐曄宍傪峫椂偟側偄応崌乯偺桿摫傕壜擻偱偁傞丅偙傟偵偮偄偰偼丆暿搑
丂丂丂丂僾儕儞僩傪攝晍偡傞丅
偙偺儁乕僕偺愭摢傊栠傞
丂乮7乯丂晹嵽儌僨儖
丂丂丂丂俼俠崪慻偺抏慪惈惈忬傪昡壙偡傞偨傔偵偼丆尩枾偵偼僐儞僋儕乕僩偺擟堄懡幉墳椡壓偺
丂丂墳椡搙乣傂偢傒搙娭學丆揝嬝偺墳椡搙乣傂偢傒搙娭學丆媦傃揝嬝偺偡傋傝摍偺庢埖傪
丂丂峫椂偡傞昁梫偑偁傞丅偟偐偟丆偙傟摍偵偮偄偰偼枹夝柧側晹暘傕懡偔丆慡偰傪峫椂偱偒偨偲
丂丂偟偰傕寁嶼婡梕検丆寁嶼帪娫偺惂栺偐傜尰抜奒偱偼偁傑傝尰幚揑偱偼側偄丅
丂丂丂丂偙偺揰傪摜傑偊偰嵽椏偺惈幙偵傑偱偝偐偺傏傞偙偲側偔丆晹嵽偺嵽抂儌乕儊儞僩乣嵽抂
丂丂夞揮妏娭學傪晹嵽幚尡偵婎偯偄偰儌僨儖壔偟丆奺嵹壸抜奒偵偍偗傞晹嵽偺弖娫崉惈儅僩
丂丂儕僢僋僗傪嶼掕偡傞曽朄偑俼俠峔憿暔偺摦揑夝愅偱偼峀偔梡偄傜傟偰偄傞丅
丂丂丂偲偙傠偱丆晹嵽偺抏慪惈惈忬傪尋媶偡傞偨傔偺幚尡偼丆捠忢恾7-1偵帵偡扨弮巟帩晹嵽
丂丂偱峴傢傟傞丅偙偺扨弮巟帩偝傟偨晹嵽偺拞墰偵壸廳俹傪偐偗偨偲偒偺俹乣兟娭學傪
丂丂俵亖俹俴乛係偲俼亖俀兟乛俴丂偺娭學偵曄姺偡傞偲丆恾7-1偺俵乣俼娭學偼恾7-2偵帵偡
丂丂媡懳徧嵽偺嵽抂儌乕儊儞僩俵偲嵽抂夞揮妏儲偲偺娭學偵捈愙懳墳偡傞丅埲忋偵傛傝丆晹嵽偺
丂丂幚尡寢壥傪摑寁揑偵惍棟偡傞摍偡傟偽丆媡懳徧嵽偵偮偄偰偺暅尦椡摿惈偼寛傔傜傟傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂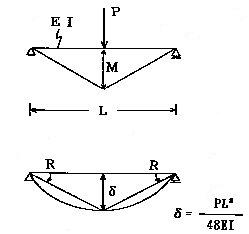
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂恾7-1丂扨弮巟帩偽傝乮拞墰廤拞壸廳乯
丂丂丂丂丂丂丂丂丂丂丂丂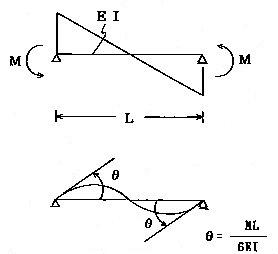
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂恾7-2丂媡懳徧嵽
丂丂丂丂堦曽丆晹嵽偺嵽抂椡偲嵽抂曄埵偺憹暘娭學偼丆弖娫崉惈儅僩儕僢僋僗傪夘偟偰師幃偺
丂丂丂傛偆偵昞偣傞丅
丂丂丂丂丂丂丂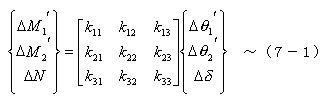
丂丂丂丂偟偐偟丆晛捠偼幉曽岦椡偵偮偄偰偼嬋偘偲暘棧偟偰榑偠傜傟丆妿偮抏惈偲壖掕偝傟傞
丂丂応崌偑懡偄丅廬偭偰丆倠侾俁亖倠俀俁亖倠俁侾亖倠俁俀亖侽偲側傞丅
丂丂丂丂媡懳徧壸廳偺応崌丆仮俵侾乫亖仮俵俀乫丆仮儲侾乫亖仮儲俀乫偱偁傞偺偱弖娫崉惈偲偟偰
丂丂倠侾侾亄倠侾俀乮亖倠俀侾亄倠22乯偲偄偆堦偮偺抣偟偐寛傔傜傟側偄丅偙傟傪傛傝堦斒揑側擟堄偺嬋偘
丂丂儌乕儊儞僩暘晍傪桳偡傞晹嵽偵傕奼挘偟丆俀尦偺弖娫崉惈儅僩儕僢僋僗傪嶌傞偨傔偵偼丆偦偺
丂丂嫶搉偟偲偟偰晹嵽儌僨儖乮倐倕倎倣丂倣倧倓倕倢乯偑昁梫偲側傞丅
丂丂丂丂埲忋偺傛偆偵丆媡懳徧晹嵽偵偮偄偰偺僇偲曄宍偲偺娭學傪昞偡乽暅尦椡摿惈儌僨儖乿偲
丂丂偙傟傪媡懳徧偱側偄堦斒偺晹嵽偵奼挘偡傞偨傔偺乽晹嵽儌僨儖乿偺俀偮偺儌僨儖傪梡偄傟偽
丂丂崪慻偺抏慪惈夝愅傪峴偆偙偲偑偱偒傞丅
丂丂丂丂埲壓偱偼丆婛墲偺尋媶偲偟偰戙昞揑側晹嵽儌僨儖偺撪丆嵽抂僶僱儌僨儖偲廮惈僷儔儃儔
丂丂儌僨儖丆媦傃晹嵽偺嬋偘儌乕儊儞僩乣嬋棪偺愝掕偐傜弌敪偡傞廮堟儌僨儖偵偮偄偰弎傋傞丅
丂乮1乯丂嵽抂僶僱儌僨儖乮One丂Component丂Model乯
丂丂丂丂M.F.Giberson偵傛傝採埬偝傟偨儌僨儖偱丆恾7-3偵帵偡傛偆偵丆晹嵽偼抏惈傪曐偮拞墰偺
丂丂丂晹嵽偲椉抂偵憓擖偝傟偨崉慪惈夞揮僶僱偐傜峔惉偝傟偰偄傞傕偺偲偡傞丅偟偨偑偭偰丆晹嵽
丂丂丂偺慪惈壔偵傛傞崉惈掅壓偼椉抂偺僶僱偵尷掕偝傟傞偨傔丆椉抂偱曄宍偼晄楢懕偲側傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂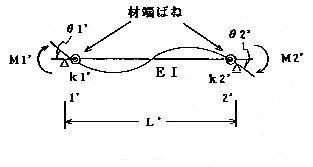
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂恾7-3丂嵽抂偽偹儌僨儖
丂丂丂丂埲忋偺壖掕傛傝丆晹嵽偺潥傒惈偼丆
丂丂丂丂丂丂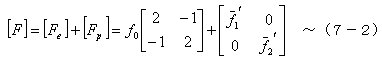
丂丂丂忋幃傪曄宍偡傞偲丆
丂丂丂丂丂丂
丂丂丂偲昞偣傞丅
丂丂丂丂偙偺慪惈僶僱偺儌乕儊儞僩偲夞揮妏偵懳偟偰暅尦椡摿惈儌僨儖傪巊梡偡傞偙偲傕偱偒傞偑丆
丂丂丂偙偺応崌偵偼晹嵽偺抏惈曄宍偑丆偦偺暅尦椡摿惈偵偼慡偔斀塮偝傟側偄偙偲偵側傞丅偦偙
丂丂丂偱丆晹嵽抂偵偍偗傞暅尦椡摿惈儌僨儖偺暅尦椡偲偟偰偼晹嵽抂儌乕儊儞僩傪偲傝丆偦偺曄埵
丂丂丂偲偟偰偼丆偦偺晹嵽抂儌乕儊儞僩偵懳偟偰斀嬋揰偑晹嵽拞墰偵偁傞応崌偵惗偢傞晹嵽偺
丂丂丂抏惈曄宍傪崌傔偨晹嵽抂夞揮妏傪梡偄傞偙偲偑懡偄丅偙傟偼丆媡懳徧嵽偺潥傒惈倖0偵慪惈
丂丂丂僶僱偺潥傒惈倖侾乫丆埥偼倖俀乫傪壛偊偨潥傒惈傪暅尦椡儌僨儖偱昡壙偡傞偙偲偱偁傞丅
丂丂丂丂丂丂丂丂丂丂丂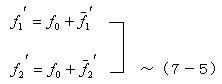
丂丂丂偙偺幃傪乮7-3乯幃偵戙擖偡傞偲丆
丂丂丂丂丂丂丂丂丂丂丂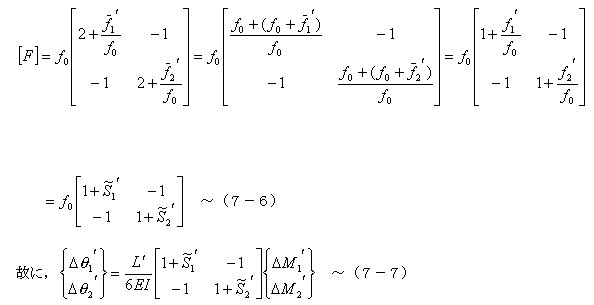
丂丂丂偱昞偝傟傞丅偙偙偵丆僥傿儖僟乕S1'丆S2'偼丆乮7-4乯幃偺S1'丆S2乫偲堎側傝斀嬋揰偑晹嵽拞墰
丂丂丂偵偁傞応崌偵惗偢傞晹嵽偺抏惈曄宍偺塭嬁暘傪娷傫偱偄傞丅偙偺僥傿儖僟乕S1'丆S2乫偺暘巕
丂丂丂傪暅尦椡摿惈偱昡壙偡傟偽椙偄丅乮7-7乯幃偺潥傒惈傪梡偄偨偙偺儌僨儖偺寚揰偼丆侾乫抂偲
丂丂丂俀乫抂偺儌乕儊儞僩偺憡屳嶌梡傪昞偡旕懳妏崁偑堦侾偱丆晹嵽偺抏惈惈忬偺傒偵埶懚偟偰
丂丂丂懠抂偺崉惈掅壓偵傛傞塭嬁偑斀塮偝傟側偄偙偲偱偁傞丅廬偭偰丆晹嵽偺懝彎偑挊偟偄応崌偵
丂丂丂偙偺儌僨儖傪梡偄傞偙偲偼晄揔摉偲側傞丅
丂丂丂丂傑偨丆乮7-7乯幃偼晹嵽偺儌乕儊儞僩暘晍偑媡懳徧偲側傞応崌偵尷偭偨偲偒偺抏惈曄宍傪崌傔
丂丂丂偨幃偱偁傞偐傜丆偙偺忦審偐傜挊偟偔堩扙偡傞応崌偵偼揔媂梊憐偝傟傞墳椡忬懺偺曄宍傪娷
丂丂丂傓幃偵廋惓偡傞昁梫傕偁傞丅
偙偺儁乕僕偺愭摢傊栠傞
丂



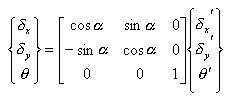

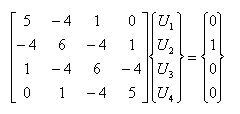
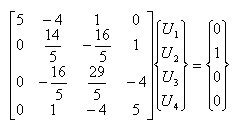
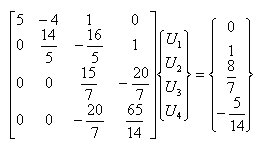
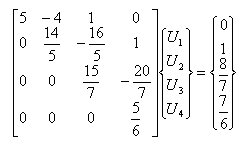
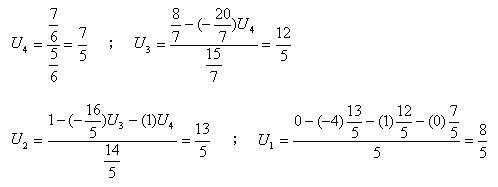

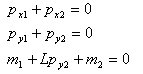
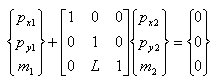

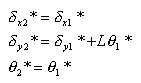
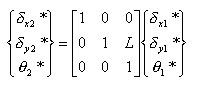
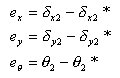

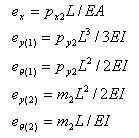
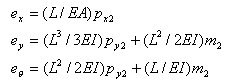
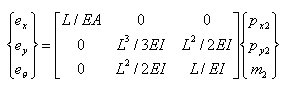
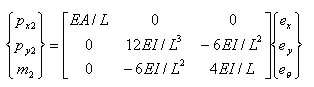
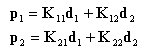
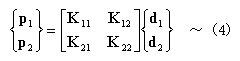
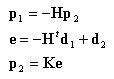
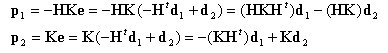
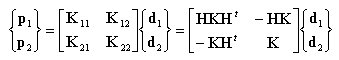

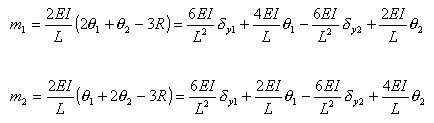
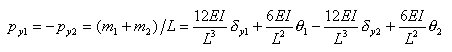

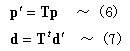
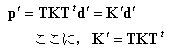
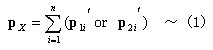
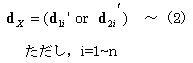
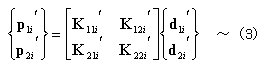
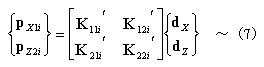




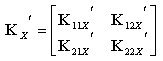

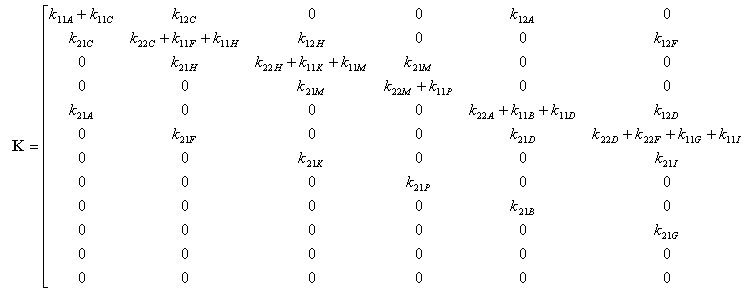
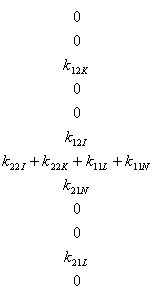 丂
丂