


Next: 2 The unperturbed disc
Up: Abstract
Previous: Abstract
Be stars are non-supergiant B-type stars with
Balmer emission lines.
The emission lines arise from a cool envelope surrounding
the star.
Interferometric observations have confirmed that
the cool envelope has a disc-like geometry
with a rotational velocity distribution
closer to a Keplerian distribution
than to a distribution in the flow with a constant angular momentum
(Mourard et al. 1989; Hirata 1994; Quirrenbach 1994; Vakili et al. 1994).
Many (but not all) Be stars exhibit long-term quasi-cyclic variations in
the relative intensities
of the violet and red components in
double-peaked Balmer emission-line profiles (V/R variations).
Typical features of V/R variations are summarized in
e.g., Dachs (1987) or Hubert (1994) and references therein
(see also Appendix).
The periods of V/R variations range from years to a decade,
which is much longer than
the rotation periods of the central stars and cool disc-like envelopes.
These periods do not depend on the spectral type of the central star.
Moreover, these periods can vary from one cycle to the next for
individual stars.
In addition, the profile as a whole shifts blueward
when the red component is stronger
and shifts redward when the violet component is stronger.
The present paper is mainly concerned with the physical mechanisms
that cause the long-term V/R variations.
A satisfactory model should account for
(1) the range of V/R periods,
(2) the dependence of the period on the properties of the Be star, and
(3) the time evolution of the V/R cycle.
Okazaki (1991) constructed a model
first suggested by Kato (1983)
in which
the long-term V/R variations are due to the phenomena caused by
global one-armed (i.e., m=1) oscillations
in the equatorial discs of Be stars.
Here, m is the azimuthal wave number.
The model is based on the theoretical result
that the low-frequency, one-armed oscillations
are the only possible global oscillations in
geometrically thin (i.e., near Keplerian) discs
(Kato 1983, 1989; Okazaki & Kato 1985; Adams et al. 1989).
Studying the linear m=1 eigenmodes
in isothermal equatorial discs,
Okazaki (1991) found that the one-armed oscillation model
well explains the observed periodicity of
the long-term V/R variations.
Since then, a number of studies which support
the one-armed oscillation model
have appeared.
Based on 3D radiative transfer calculations,
Hummel & Hanuschik (1994, 1996) showed that
calculated line profiles from discs
with m=1 perturbation patterns agree with observed line-profile
variability.
Using high-resolution H and Fe II spectroscopic data
of five selected Be stars,
Hanuschik et al. (1995) demonstrated that the one-armed oscillation
model can account for the asymmetric profile shapes as well as
the profile variations.
Hummel & Vrancken (1995) analysed the line-profile shapes
of Be stars in detail and derived several kinematical and
geometrical constraints on the structure of individual discs.
They found strong evidence that the asymmetric profiles
originate from discs with an eccentric (i.e., m=1) density
distribution.
Moreover, Telting et al. (1994) clearly demonstrated that
the long-term variability
of Balmer lines of the Be star
and Fe II spectroscopic data
of five selected Be stars,
Hanuschik et al. (1995) demonstrated that the one-armed oscillation
model can account for the asymmetric profile shapes as well as
the profile variations.
Hummel & Vrancken (1995) analysed the line-profile shapes
of Be stars in detail and derived several kinematical and
geometrical constraints on the structure of individual discs.
They found strong evidence that the asymmetric profiles
originate from discs with an eccentric (i.e., m=1) density
distribution.
Moreover, Telting et al. (1994) clearly demonstrated that
the long-term variability
of Balmer lines of the Be star 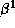 Mon is caused
by a prograde one-armed density structure in the disc.
In addition, the following circumstantial evidence also seems to
support the one-armed oscillation model:
The activity of discrete absorption components in the stellar wind
of
Mon is caused
by a prograde one-armed density structure in the disc.
In addition, the following circumstantial evidence also seems to
support the one-armed oscillation model:
The activity of discrete absorption components in the stellar wind
of 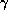 Cas is associated with the cyclic V/R variability
(Doazan et al. 1987; Telting & Kaper 1994).
Telting & Kaper (1994) found that
this correlation is consistent with the one-armed oscillation model.
Cas is associated with the cyclic V/R variability
(Doazan et al. 1987; Telting & Kaper 1994).
Telting & Kaper (1994) found that
this correlation is consistent with the one-armed oscillation model.
In the one-armed oscillation model, the slow pattern speed of
the m=1 density wave results from the slight deviation
of the rotational velocity distribution in the disc
from the Keplerian distribution.
Okazaki (1991) considered the pressure force in the disc
as the only mechanism
that gives rise to this deviation.
In such a disc, the m=1 waves can propagate throughout the disc.
This means that the period of the finite-order m=1 mode
asymptotically goes to infinity as the disc size goes to infinity.
In order to make oscillation periods finite,
Okazaki (1991) needed to impose a disc outer radius and
obtained the spectrum of the retrograde eigenmodes
of which the periods depend on the size of the disc outer radius.
When the disc outer radius is 5-20 stellar radii,
the periods of the eigenmode agreed with the observed period range of
V/R variations.
At present, however,
imposing an outer radius to avoid the confinement problem
seems inadequate,
because there is no observational evidence that
the edge of the H emitting region is also
the edge of the equatorial disc,
although the above range
covers the observed sizes of H
emitting region is also
the edge of the equatorial disc,
although the above range
covers the observed sizes of H emitting regions quite well.
On the contrary, from IR and radio observations,
the discs seem to extend far beyond the area
where the H
emitting regions quite well.
On the contrary, from IR and radio observations,
the discs seem to extend far beyond the area
where the H emission arises (Waters et al. 1991).
Moreover, the prograde one-armed density structure
found in the disc of
emission arises (Waters et al. 1991).
Moreover, the prograde one-armed density structure
found in the disc of 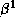 Mon (Telting et al. 1994)
cannot be explained by Okazaki's model.
Mon (Telting et al. 1994)
cannot be explained by Okazaki's model.
Papaloizou et al. (1992, henceforth PSH) pointed out this shortcoming
of Okazaki's model and suggested that
prograde one-armed oscillations are confined to
the inner part of Be-star discs by
including the quadrupole contribution to the potential of the star
which is distorted by the rapid rotation.
Savonije & Heemskerk (1993, henceforth SH) constructed
a model in which the effect of the rotational deformation is much stronger
than the pressure effect,
and obtained the results that
confirm the above conclusion of PSH.
In their studies, however,
the effect of the rotational deformation of the star is
overestimated by the pressure effect being underestimated.
The range of the disc temperature they studied
is too low to apply to Be-star discs.
PSH adopted 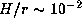 ,
where r is the distance from the stellar center and
H the half-thickness of the disc.
This value of disc thickness corresponds to a disc temperature
,
where r is the distance from the stellar center and
H the half-thickness of the disc.
This value of disc thickness corresponds to a disc temperature
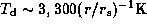 for a B0-type star and
for a B0-type star and
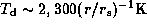 for a B5-type star,
where
for a B5-type star,
where 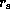 is the stellar radius.
Even in the innermost region of the disc,
the disc temperature PSH adopted
is thus about an order of magnitude lower
than typical temperatures of Be-star discs.
SH studied m=1 oscillations
in discs with
is the stellar radius.
Even in the innermost region of the disc,
the disc temperature PSH adopted
is thus about an order of magnitude lower
than typical temperatures of Be-star discs.
SH studied m=1 oscillations
in discs with 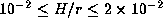 around a star of
around a star of 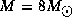 and
and 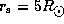 .
This parameter range covers
.
This parameter range covers
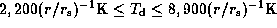 ,
which is also too low to apply to Be-star discs.
Consequently, it is worth examining
the effect of the rotational deformation of the central star
to investigate whether
it is large enough to give rise to the confinement of m=1 oscillations
in the inner part, say
,
which is also too low to apply to Be-star discs.
Consequently, it is worth examining
the effect of the rotational deformation of the central star
to investigate whether
it is large enough to give rise to the confinement of m=1 oscillations
in the inner part, say 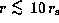 , of the discs
of Be stars.
, of the discs
of Be stars.
Since the proposal of the rotation hypothesis for Be stars
by Struve (1931),
many studies have been done to test this hypothesis
[see Slettebak (1976) for a historical review].
Statistical studies of the distribution of rotation velocities
of Be stars have basically confirmed the rotation hypothesis.
They have also revealed, however, that
the rapid rotation cannot be the sole factor
responsible for the Be phenomena
(Massa 1975; Slettebak 1976; Fukuda 1982; Kogure & Hirata 1982).
Be stars rotate significantly below the critical velocity.
The ratio of the rotation velocity to the critical velocity
(the rotation parameter) is, on average, smaller for earlier-type
Be stars [see Fig. 4 of Kogure & Hirata (1982),
and other references].
The distribution of the rotation velocities of Be stars
earlier than B3 mostly overlaps that of normal B stars,
while Be stars in the spectral range B3--B9 have rotation velocities
distinctly higher than normal B stars.
This property, together with the observed fact that
the fraction of Be stars among B stars has a maximum at B2
(Kogure & Hirata 1982),
strongly suggests that
another mechanism also has to work to trigger the Be phenomena,
at least in the spectral range B0--B2.
It is the radiative force that we consider to be
the promising candidate.
If the radiative force plays an important role for the Be phenomena,
it should also have a strong influence on
the confinement of the one-armed oscillations in Be-star discs.
The purpose of this paper is to examine the effects of
the radiative force and the rotational deformation of the star
on the confinement of one-armed oscillations in Be-star discs.
Since the radial flow in the inner part of the Be-star disc is
considered to be subsonic (Hanuschik 1994),
the radiative force in the disc would arise not from
the optically-thick strong lines
but from an ensemble of optically-thin weak lines
(and from the optically-thin continuum).
Hence, for the radiative force, we adopt the parametric form
proposed by Chen & Marlborough (1994).
Examining the eigenvalue problem
for a wide range of parameters
characterizing the effects of rotation and radiation,
we find that, in late-type Be stars,
the effect due to rotational deformation of the star
is the cause for the confinement of m=1 oscillations.
Our results thus show that
the mechanism proposed by PSH and confirmed by SH
effectively works in discs around late-type Be stars.
We also find, however, that the rotational effect is much less
important in discs of early-type Be stars.
For these stars, it is the weak line force
that mainly contributes to the confinement of the m=1 oscillations.
Finally, we compare our results with observed V/R cycles
of an extensive number of stars.



Next: 2 The unperturbed disc
Up: Abstract
Previous: Abstract
Atsuo Okazaki
平成9年3月15日 (土), 午後 1時19分3秒
 and Fe II spectroscopic data
of five selected Be stars,
Hanuschik et al. (1995) demonstrated that the one-armed oscillation
model can account for the asymmetric profile shapes as well as
the profile variations.
Hummel & Vrancken (1995) analysed the line-profile shapes
of Be stars in detail and derived several kinematical and
geometrical constraints on the structure of individual discs.
They found strong evidence that the asymmetric profiles
originate from discs with an eccentric (i.e., m=1) density
distribution.
Moreover, Telting et al. (1994) clearly demonstrated that
the long-term variability
of Balmer lines of the Be star
and Fe II spectroscopic data
of five selected Be stars,
Hanuschik et al. (1995) demonstrated that the one-armed oscillation
model can account for the asymmetric profile shapes as well as
the profile variations.
Hummel & Vrancken (1995) analysed the line-profile shapes
of Be stars in detail and derived several kinematical and
geometrical constraints on the structure of individual discs.
They found strong evidence that the asymmetric profiles
originate from discs with an eccentric (i.e., m=1) density
distribution.
Moreover, Telting et al. (1994) clearly demonstrated that
the long-term variability
of Balmer lines of the Be star 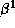 Mon is caused
by a prograde one-armed density structure in the disc.
In addition, the following circumstantial evidence also seems to
support the one-armed oscillation model:
The activity of discrete absorption components in the stellar wind
of
Mon is caused
by a prograde one-armed density structure in the disc.
In addition, the following circumstantial evidence also seems to
support the one-armed oscillation model:
The activity of discrete absorption components in the stellar wind
of 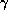 Cas is associated with the cyclic V/R variability
(Doazan et al. 1987; Telting & Kaper 1994).
Telting & Kaper (1994) found that
this correlation is consistent with the one-armed oscillation model.
Cas is associated with the cyclic V/R variability
(Doazan et al. 1987; Telting & Kaper 1994).
Telting & Kaper (1994) found that
this correlation is consistent with the one-armed oscillation model.
 emitting region is also
the edge of the equatorial disc,
although the above range
covers the observed sizes of H
emitting region is also
the edge of the equatorial disc,
although the above range
covers the observed sizes of H emitting regions quite well.
On the contrary, from IR and radio observations,
the discs seem to extend far beyond the area
where the H
emitting regions quite well.
On the contrary, from IR and radio observations,
the discs seem to extend far beyond the area
where the H emission arises (Waters et al. 1991).
Moreover, the prograde one-armed density structure
found in the disc of
emission arises (Waters et al. 1991).
Moreover, the prograde one-armed density structure
found in the disc of 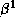 Mon (Telting et al. 1994)
cannot be explained by Okazaki's model.
Mon (Telting et al. 1994)
cannot be explained by Okazaki's model.
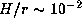 ,
where r is the distance from the stellar center and
H the half-thickness of the disc.
This value of disc thickness corresponds to a disc temperature
,
where r is the distance from the stellar center and
H the half-thickness of the disc.
This value of disc thickness corresponds to a disc temperature
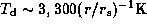 for a B0-type star and
for a B0-type star and
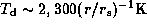 for a B5-type star,
where
for a B5-type star,
where 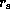 is the stellar radius.
Even in the innermost region of the disc,
the disc temperature PSH adopted
is thus about an order of magnitude lower
than typical temperatures of Be-star discs.
SH studied m=1 oscillations
in discs with
is the stellar radius.
Even in the innermost region of the disc,
the disc temperature PSH adopted
is thus about an order of magnitude lower
than typical temperatures of Be-star discs.
SH studied m=1 oscillations
in discs with 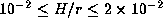 around a star of
around a star of 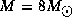 and
and 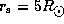 .
This parameter range covers
.
This parameter range covers
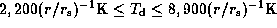 ,
which is also too low to apply to Be-star discs.
Consequently, it is worth examining
the effect of the rotational deformation of the central star
to investigate whether
it is large enough to give rise to the confinement of m=1 oscillations
in the inner part, say
,
which is also too low to apply to Be-star discs.
Consequently, it is worth examining
the effect of the rotational deformation of the central star
to investigate whether
it is large enough to give rise to the confinement of m=1 oscillations
in the inner part, say 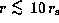 , of the discs
of Be stars.
, of the discs
of Be stars.