

 Astronomical Institute 'Anton Pannekoek',
University of Amsterdam,
Kruislaan 403,
1098 SJ Amsterdam,
The Netherlands
Astronomical Institute 'Anton Pannekoek',
University of Amsterdam,
Kruislaan 403,
1098 SJ Amsterdam,
The Netherlands
Lee et al. (1991) proposed the viscous decretion disc scenario
for Be stars, in which the matter ejected from the star
drifts outward because of the effects of viscosity.
In this paper, we examine the characteristics of outflow
in viscous decretion discs around Be stars.
For simplicity, we assume the disc to be isothermal,
and adopt the  -description for the viscous stress.
As the radiative force,
we adopt the parametric form proposed by Chen and Marlborough (1994).
We also include the quadrupole contribution to the potential
around the rotationally-distorted central star,
following to Papaloizou et al. (1992) and Savonije and Heemskerk (1993).
-description for the viscous stress.
As the radiative force,
we adopt the parametric form proposed by Chen and Marlborough (1994).
We also include the quadrupole contribution to the potential
around the rotationally-distorted central star,
following to Papaloizou et al. (1992) and Savonije and Heemskerk (1993).
Solving the resultant wind equation for a wide range of parameter values,
we found that a transonic solution exists for any  .
The sonic radius is located at
.
The sonic radius is located at 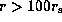 for plausible values of parameters,where
for plausible values of parameters,where 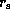 is the stellar radius.
It is smaller for higher temperature and/or larger radiative force.
We found also that
the topology of the sonic point is a node for
is the stellar radius.
It is smaller for higher temperature and/or larger radiative force.
We found also that
the topology of the sonic point is a node for 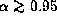 ,
while it is a saddle for
,
while it is a saddle for 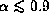 .
According to the theory of accretion,
the sonic point in the former case is unstable,
while that in the latter case is stable
(e.g., Abramowicz and Kato 1989).
.
According to the theory of accretion,
the sonic point in the former case is unstable,
while that in the latter case is stable
(e.g., Abramowicz and Kato 1989).
Figure 1 shows the typical structure of
the viscous transonic decretion disc.
We note that the outflow is highly subsonic
in the inner part of the disc.
We note also that, in the subsonic region, the outflow velocity
increases as r and
the local density decreases as 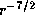 .
The angular velocity of the disc decreases as
.
The angular velocity of the disc decreases as 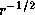 in the inner subsonic region,
while it decreases as
in the inner subsonic region,
while it decreases as 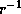 in the outer subsonic region.
in the outer subsonic region.
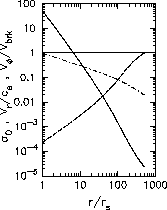
Figure 1: Structure of the viscous transonic disc around a B0V star.
The disc temperature is assumed to be 2/3 of
the effective temperatur
e of the star.
The value of  is 0.1.
The solid, dashed, and dash-dotted lines denote
the surface density in units of
is 0.1.
The solid, dashed, and dash-dotted lines denote
the surface density in units of 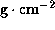 ,
the Mach number of the outflow,
and the angular velocity of the disc normalized by
the break-up velocity.
Though the surface density is calculated for the mass decretion rate
of
,
the Mach number of the outflow,
and the angular velocity of the disc normalized by
the break-up velocity.
Though the surface density is calculated for the mass decretion rate
of 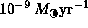 ,
the velocity distribution is independent of the mass decretion rate.
The other parameters are:
the deformation factor
,
the velocity distribution is independent of the mass decretion rate.
The other parameters are:
the deformation factor 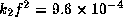 and
the weak line force in the form of
and
the weak line force in the form of
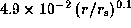 .
.
Many Be stars exhibit long-term V/R variations, which are considered to be caused by the variations in the equatorial discs (e.g., Poeckert 1982). It is thus important to investigate the characteristics of the oscillation modes in viscous decretion disc discussed above. Since the possible global oscillations in near Keplerian discs are one-armed oscillations alone (e.g., Kato 1983), we restrict our attention to the one-armed oscillation mode. For simplicity, the oscillation is assumed to be linear.
Figure 2 shows an example of the one-armed fundamental mode confined in the inner part of the viscous transonic decretion disc. It is important to note that the characteristics of the one-armed spiral mode are consistent with the periodicity and line profile variability of the observed V/R variations. Note also that the mode is a leading one-armed spiral wave. This suggests that the V/R asymmetry in the individual lines would progressively shift with time from lower to higher Balmer members.
The one-armed oscillation modes in viscous decretion discs are, in general, overstable because of the viscous effect. The period and the growth time are roughly comparable.
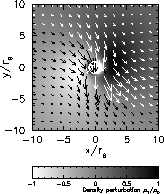
Figure 2: One-armed fundamental mode confined in the inner part of
the viscous transonic decretion disc.
The gray-scale plot denotes the density perturbation 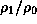 on the equatorial plane,
while arrows denote the perturbed velocity vectors
relative to the local angular velocity of the unperturbed disc.
on the equatorial plane,
while arrows denote the perturbed velocity vectors
relative to the local angular velocity of the unperturbed disc.
References
Abramowicz, M.A., and Kato, S. 1989, ApJ 336, 304.
Chen, H., Marlborough, J.M. 1994, ApJ 427, 1005.
Kato, S. 1983, PASJ 35, 249.
Lee, U., Saio, H., and Osaki, Y. 1991, MNRAS 250, 432.
Papaloizou, J.C., Savonije, G.J., Henrichs, H.F. 1992, A&A 265,L45.
Poeckert, R. 1982, in Be stars, IAU Symp. No.98, ed M. Jaschek, H.-G. Groth (D. Reidel Publishing Company, Dordrecht), p. 453.
Savonije, G.J., Heemskerk, M.H.M. 1993, A&A 276, 409.